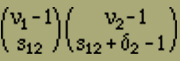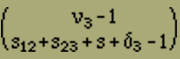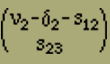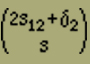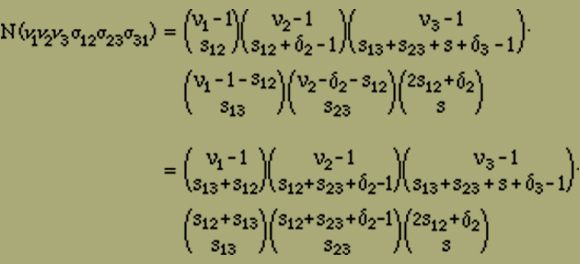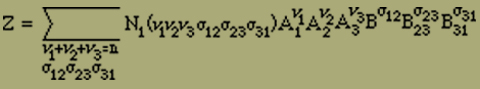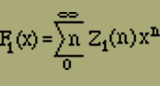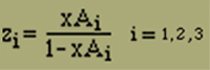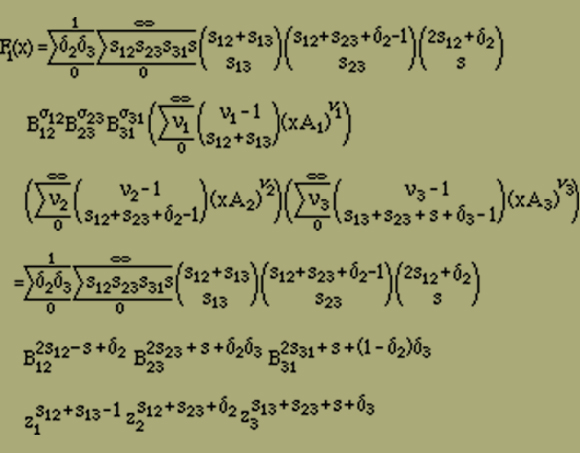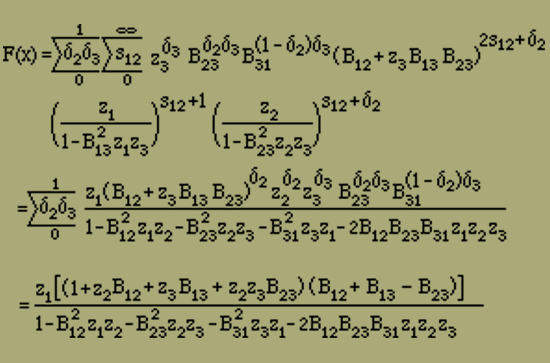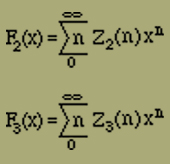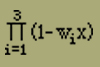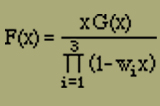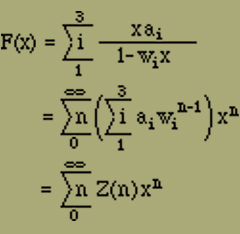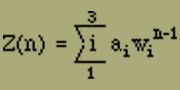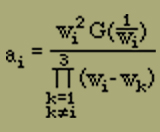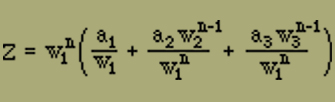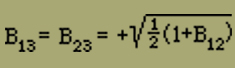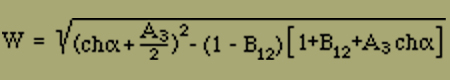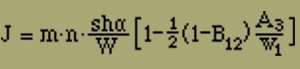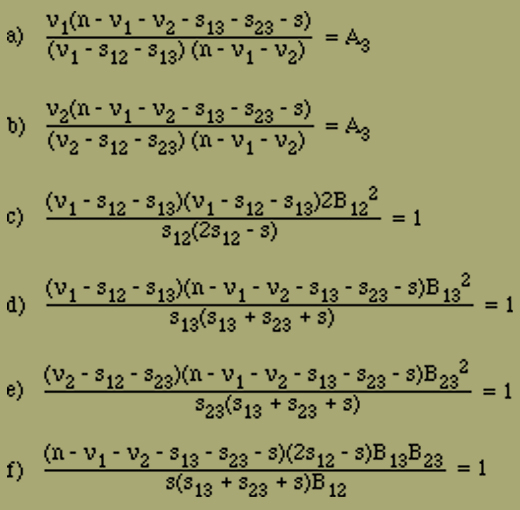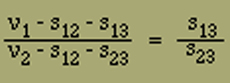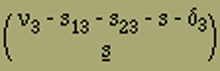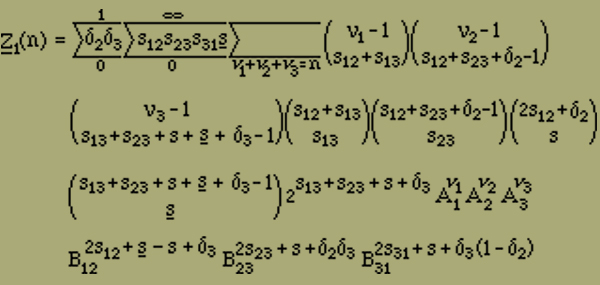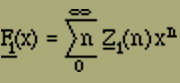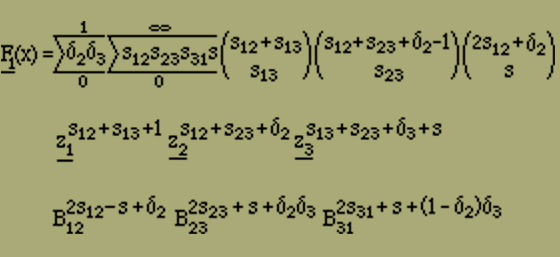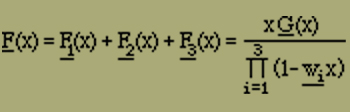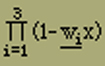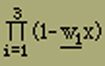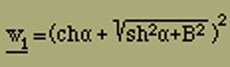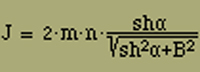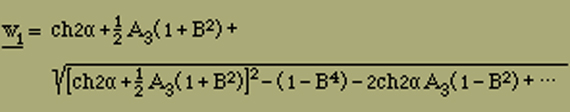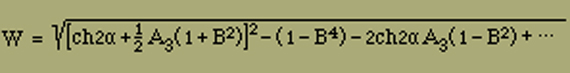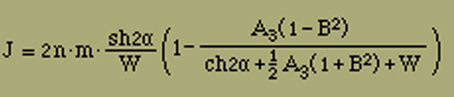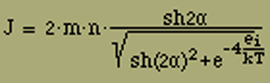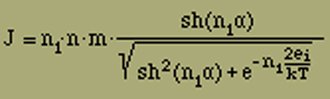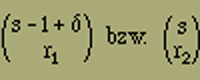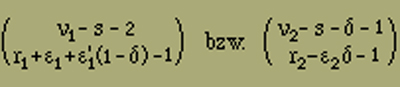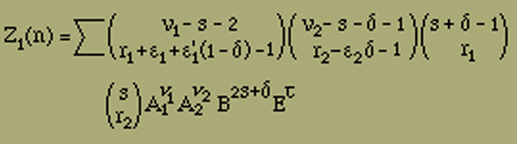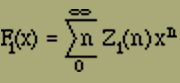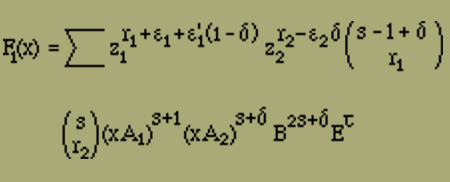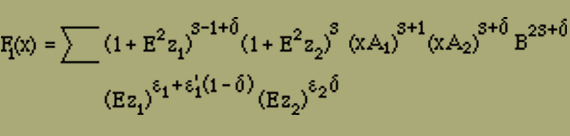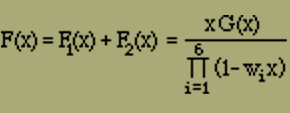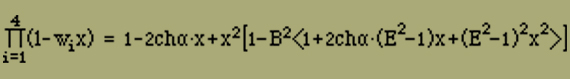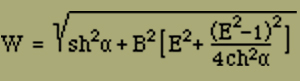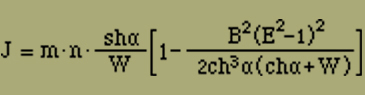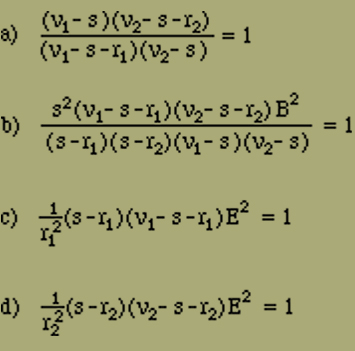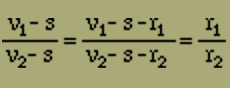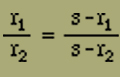BIBLIOTHECA AUGUSTANA
Ernst Ising
1900 - 1998
Beitrag zur Theorie desFerro- und Paramagnetismus
1924
|
|||||||||||||||||
|
____________________________________________________________
|
|||||||||||||||||
Hauptteil
II.Kompliziertere Fälle.
――――――――――
§ 6.Die lineare Kette bei Zulassungvon Querstellungen.
a) Die Anordnungsmöglichkeiten.
Mittels der bisher betrachteten Modelle gelangen wir unter den am Anfang gemachten Annahmen nur zu einer Erklärung des Ferromagnetismus und es ist möglich, dass vielleicht nur eine zu grosse Idealisierung ein ferromagnetisches Verhalten nicht in Erscheinung treten liess. Es ist ja denkbar, dass ein räumliches Modell, bei dem alle irgendwie benachbarten Elemente auf einander wirken, die nötige Stabilität mit sich bringt, um zu verhindern, dass die Magnetisierungsintensität mit H verschwindet. Doch es scheint in diesem Fall die Rechnung nicht durchführbar zu sein; jedenfalls ist es bisher nicht gelungen, die Anordnungsmöglichkeiten geeignet zu sortieren und abzuzählen. Um uns jedoch einen Ueberblick über die Verhältnisse zu verschaffen, wollen wir jetzt die folgenden drei Betrachtungen durchführen, in denen wir gewisse vereinfachende Annahmen des Früheren fallen lassen.Wir müssen annehmen, dass die Elemente in einem ferromagnetischen Kristall nicht nur 2 verschiedene Stellungen einnehmen können, wie wir es bisher angesetzt haben. Wir wollen deshalb jetzt untersuchen, welchen Einfluss es hat, wenn wir weitere Stellungen neben der positiven und negativen zulassen. Wir betrachten wieder einen linearen Magneten, bestehend aus r Elementen. Jedes dieser Elemente soll aber jetzt ausser den beiden Längsstellungen parallel der Kette noch r weitere Stellungen senkrecht zur Ausdehnungsrichtung einnehmen können, die wir kurz Querstellungen nennen wollen. Die Anzahl r lassen wir zunächst unbestimmt, da dadurch die Rechnung nicht komplizierter wird. Wir müssen jedoch annehmen, dass r geradzahlig ist, da keine Richtung vor der entgegengesetzten ausgezeichnet sein soll. Denken wir an die sechszählige Achse des Pyrrhotin als Längsrichtung, so ist r=6; bei Magnetit dagegen haben wir r=4 zu setzen, entsprechend der vierzähligen Symmetrie der Achsen. Die r Querstellungen seien alle gleichberechtigt.Wir müssen vor allen Dingen wissen, wie viel Stellungen möglich sind mit ν1 positiven, ν2 negativen und ν3 quergestellten Elementen - ν1+ν2+ν3=n - und mit σ12, σ23 bzw. σ31 Energiestellen zwischen positiven und negativen, negativen und quergestellten bzw. quergestellten und positiven Elementen. Es ist wieder zweckmässig, zunächst unter diesen Anordnungen nur die zu zählen, deren erstes Element links positiv gerichtet ist. Durch zyklische Vertauschung der Indizes 1, 2, 3 erhält man später die Anzahl der mit einem negativen bzw. quergestellten Element beginnenden Anordnungen. Bei der Abzählung verfahren wir zunächst wie oben im Fall ohne Querstellungen. Wir denken die ν1 positiven Elemente in einer Reihe angeordnet, zwischen ihnen verteilen wir an s12 Punkten je zwei Energiestellen, wie sie zwischen positiven und negativen Elementen auftreten, und, falls δ2=1 ist, eine weitere am rechten Ende. Dazwischen ordnet man schliesslich die negativen Elemente an. Die Anzahl dieser Anordnungen beträgt nach der Gleichung (12)
|
|||||||||||||||||
(23) |
Was die Verteilung der Energiestellen anbetrifft, so sind an ausgewählten s13, s23 und s Punkten je zwei Energiestellen, wie sie zwischen quergestellten und positiven bzw. negativen Elementen auftreten, einzufügen, und eine weitere, falls δ2δ3 oder (1-δ2)δ3 gleich 1 ist. Natürlich sind an den Stellen, wo zunächst positive und negative Elemente sich gegenüber standen und jetzt quergestellte Elemente eingeführt sind, die ursprünglichen Energiestellen zu entfernen. Diese Bemerkung ist sebstverständlich für die Abzählung der Anordnungsmöglichkeiten belanglos. Danach erhalten wir für die Anzahl der Energiestellen zwischen positiven und negativen, negativen und quergestellten bzw. quergestellten und positiven Elementen
σ12 = 2s12-s+δ2
σ23 = 2s23+s+δ2δ3
bzw.
σ31 = 2s31+s+(1-δ2)δ3
b) Die Summationen.
Die Berechnung des mittleren Moments erfolgt nun in genau der gleichen Weise wie früher. Man hat zunächst die Zustandssumme
(24) |
zu bilden. A1 und A2 haben die alte Bedeutung.
A1 = eα
A2 = e-α
α = (|m|H / kT)
A3 = re-(ea/kT)
wobei ea die äussere Energie bezeichnet, die eine Querstellung erfordert. Die Grössen Bik rühren von der inneren Energie her. Es ist
Bik = e-(eik/kT)
e12, e23 bzw. e31 ist die Energie, die auftritt, wenn an einer Stelle ein positives und negatives, ein negatives und quergestelltes bzw. ein quergestelltes und positives Element zusammen stossen.
Es ist über ν1+ν2+ν3=n und über σ12, σ23, σ31 oder über s12, s23, s31 und s von 0 bis unendlich zu summieren, denn für zu grosse Werte von sik und s verschwinden die Binomialkoeffizienten. Die Summationen lassen sich wieder bequem ausführen, wenn man Z1 als Funktion von n betrachtet und
bildet. Dadurch ist die Nebenbedingung ν1+ν2+ν3=n beseitigt, denn wir können jetzt über ν1, ν2, und ν3 unabhängig von einander von 0 bis unendlich summieren. Diese drei Summationen lassen sich in gleicher Weise mit Hilfe von Gleichung (11) ausführen, und man erhält, wenn man vorübergehend
setzt,
Jetzt lassen sich die Summationen über s, s13 und s23 mit Hilfe des Binomischen Satzes erledigen. Wir finden
Wir haben bisher nur die Anordnungen berücksichtigt, deren erstes Element links positiv ist. Die Anordnungen, die links mit einem negativen Element bzw. einem quergestellten Element beginnen, erhalten wir bei dem obigen Verfahren, wenn wir zunächst die negativen bzw. quergestellten Elemente anordnen und nachträglich die übrigen einfügen. Die zugehörigen Zustandssummen Z2 und Z3 gehen folglich aus Z1 durch zyklische Vertauschung der Indizes 1, 2, 3 hervor. Das Entsprechende gilt auch von den Funktionen
Um also jetzt sämtliche Anordnungen zu berücksichtigen, bilden wir
F(x) = F1(x) + F2(x) + F3(x)
F(x) = Zähler/Nenner
Dabei ist, da sich der Nenner von F1(x) bei beliebiger Vertauschung der Indizes nicht ändert der
Nenner = 1 - B122z1z2 - B232z2z3 - B312z3z1 - 2B12B23B31z1z2z3
und der
Zähler = z1 + z2 + z3 + 2(z1z2B12 + z2z3B23 + z3z1B31) + z1z2z3[2(B12B23 +
B23B31 + B31B12) - (B122 + B232 + B312)]
Wir gehen jetzt wieder auf x zurück, indem wir für die Abkürzung zi die Werte xAi / 1-xAi einsetzen und gleichzeitig Zähler und Nenner mit
erweitern. Dabei erhalten wir F(x) in der Form
Wir haben den Nenner, der eine Funktion 3ten Grades von x ist, sogleich in seine drei Linearfaktoren zerlegt, was für das Folgende nützlich ist. Die Grössen wi sind aus der Gleichung
= 1- x[A1 + A2 + A3] + x2[A1A2(1 - B122) +A2A3(1 - B232) + A3A1(1 - B312)] -x3A1A2A3[1 - (B122 + B232 + B312) + 2B12B23B31] |
zu bestimmen.
Für die Funktion G(x) des Zählers, die im Folgenden keine grosse Rolle spielen wird, finden wir
G(x) = [A1 + A2 + A3] - 2x[A1A2(1 - B12) + A2A3(1 - B23) + A3A1(1 - B31)] +
x2A1A2A3[3 - 2(B12 + B23 + B31) + 2(B12B23 + B23B31 + B31B12) -
(B122 + B232 + B312)]
Die Gesamtzustandssumme
Z(n) = Z1(n) + Z2(n) + Z3(n)
gewinnt man als Koeffizienten von xn bei einer Entwicklung von F(x) nach Potenzen von x. Mittels Partialbruchzerlegung erhalten wir
folglich ist
von den Zählern der Partialbrüche
lässt sich durch längere Betrachtung zeigen, dass sie analog wie früher im Wesentlichen mit wi übereinstimmen.
Wie bei Gleichung (9) gilt auch hier für das mittlere magnetische Moment J
J = m (d / dα) log Z
Diese Gleichung können wir jedoch im Allgemeinen etwas vereinfachen. Wir verstehen unter w1 die für grosse Werte von α grösste der drei Wurzeln wi und schreiben
wobei wir nur w1n ausgeklammert haben; danach liefert der Faktor von w1n bei der logarithmischen Ableitung nur einen zu vernachlässigenden Beitrag, so dass
J = m · n (d / dα) log w1
Es genügt für unsere Zwecke, in einem speziellen Fall den Wert von w1 und damit den Ausdruck von J näher zu betrachten. Um möglichst einfach zum Ziel zu kommen, wollen wir versuchen, ob es gelingt, bei plausiblen Annahmen über die Wechselwirkungsenergie eine der drei Grössen wi zum Verschwinden zu bringen.
Zunächst einmal müssen wir aus Symmetriegründen annehmen, dass es dieselbe innere Energie erfordert, wenn ein positives oder ein negatives Element mit einem quergestellten zusammenkommt, d.h. B13=B23. Setzt man dann in
den Koeffizienten von x3 gleich 0, so findet man
Dieser Wert liegt mit B12 immer zwischen 0 und 1 und ist in diesem Bereich immer grösser als B12, was besagt, da
Bik= e-(eik / kT)
ist, dass die Wechselwirkung zwischen einem positiven und negativen Element grösser ist als die zwischen einem quergestellten und einem negativen oder positiven Element. Der angegebene Wert ist also für unsere Zwecke brauchbar. Führen wir diesen Wert jetzt in F(x) ein, so steht im Nenner
= 1 - x[A1+A2+A3]+x2(1-B12)[1+B12+A3/2(A1+A2)] |
wobei wegen Gleichung (14)
A1 · A2 = 1,
A1 + A2 = 2chα
und
A3 = re-ea/kT
ist.
Aus dieser Gleichung erhalten wir,
w1 = chα + A3/2 + W
wo
Für die Intensität der Magnetisierung finden wir
(19a) |
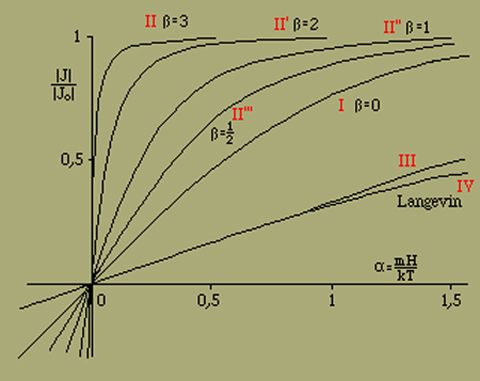
vgl. Fig. 7, Kurve III:
Fig. 7.
Das Resultat hat sich nur unwesentlich gegenüber dem Fall ohne Querstellungen geändert. Die Kurve zeigt jetzt für kleine Werte von α einen weniger steilen, aber immer noch ungefähr geradlinigen Anstieg. Nehmen wir an, dass ea und e12 sehr klein sind, so finden wir für das mittlere Moment pro Element, solange α hinreichend klein ist,
|m| = (|m|2H / kT)(2 / r+2)
Ist speziell r = 4, d.h. die Elemente haben kubische Symmetrie, so ist
|m| = |m|2H / 3kT
Wir erhalten damit den Faktor 1/3, wie er auch bei Langevin auftritt.
c) Diskussion der Maxima-Eigenschaften.
Weiter sehen wir, dass auch in dem jetzt behandelten Fall das mittlere Moment J mit dem äusseren Feld verschwindet, wie es nach dem zu Anfang des Paragraphen 4b Gesagten nicht anders zu erwarten ist. Wir wollen uns jedoch jetzt wiederum davon überzeugen, dass dieses Verschwinden nicht etwa nur vorgetäuscht wird als Folge der statistischen Mittelung über alle möglichen Lagen. Zu diesem Zweck zeigen wir, dass für den Fall H=0 aus den Gleichungen zur Bestimmung der Maximawahrscheinlichkeit die Beziehung
ν1 = ν2
folgt, d.h. aber nach Gleichung (2), dass bei der wahrscheinlichsten Anordnung das Moment mit dem äusseren Felde verschwindet. Wir können uns darauf beschränken, die Wahrscheinlichkeiten der Anordnungen zu vergleichen, deren erstes Element links positiv ist. Das ist eine für das Ergebnis unwesentliche Einschränkung. Sie bietet uns aber den Vorteil, dass wir die Wahrscheinlichkeiten sofort angeben können. Dieselben sind nach Gleichung (5 und 24)
w1(ν1ν2ν3σ12σ23σ31) = 1/Z1 · N1(ν1ν1ν1σ12σ23σ31) ·
A1ν1A2ν2A3ν3B12σ12B23σ23B31σ31
Durch die Grössen ν1, ν2, ν3, σ12, σ23, σ31 sind die betreffenden Anordnungen, zu denen diese Wahrscheinlichkeiten gehören, charakterisiert. Die Nebenbedingung
ν1 + ν2 + ν3 = n
berücksichtigen wir, indem wir
ν3 = n - ν1 - ν2
Wir werden im Folgenden Grössen von der Ordnung 1 neben ν1, ν2, s12, s23, s31 und s vernachlässigen, da letztere im Allgemeinen mit n vergleichbar sind. Die Maxima der Wahrscheinlichkeiten findet man, wenn man die Werte von ν1, ν2, s12, s23, s31 und s aufsucht, für die die Faktoren gleich 1 werden, mit denen sich die Wahrscheinlichkeiten multiplizieren, wenn wir eine dieser Zahlen um 1 vergrössern. Wir erhalten dabei folgende Gleichungen:
Wir müssen wie früher die Annahme machen
B13 = B23
Eigentlich hätten wir dieses Gleichgewichtssystem vollständig aufzulösen. Wir beschränken uns jedoch darauf, folgendes festzustellen. Die Division von a) durch b) ergibt
Weiter findet man aus d) und e)
Aus diesen beiden Proportionen folgt bereits
s13 = s23
und damit
ν1 = ν2,
was wir ja zeigen wollten. Wir sehen damit, dass das Verschwinden des mittleren Momentes wesentlich durch unseren Ansatz bedingt ist und nicht durch die Mittelbildung über lange Beobachtungszeiten.
§ 7.
Die Doppelkette bei gleichzeitiger Wirkung
benachbarter Elemente derselben
und verschiedener Ketten.
Die Betrachtungen des vorigen Paragraphen lassen sich durch einige kleine Abänderungen auch für eine Doppelkette verwerten, deren Elemente wieder nur die beiden Stellungen parallel den Ketten einnehmen können. Dafür aber soll jetzt gleichzeitig die Wechselwirkung zwischen benachbarten Elementen sowohl derselben als auch verschiedener Ketten berücksichtigt werden. In den folgenden Betrachtungen fassen wir immer zwei benachbarte, nebeneinander liegende Elemente aus den beiden Ketten zu einem Gebilde, einem Element oder besser gesagt, Elementpaar, zusammen. Wir wollen also jetzt unter den früheren positiven und negativen Elementen Paare von positiven und negativen Elementen verstehen, während wir uns unter den früheren quergestellten Elementen sogenannte positiv-negative Elementpaare, bestehend aus einem positiven und einem negativen Element denken wollen. Wir haben dementsprechend zu setzen
A1 = e2α
A2 = e-2α
A3 = e-ei / kT
ei ist die innere Energie, die erforderlich ist, um von zwei nebeneinander liegenden gleichgerichteten Elementen verschiedener Ketten eines umzuklappen. Dadurch, dass wir in A3 den Faktor r = 1 gesetzt haben, tun wir zunächst so, als ob die positiv-negativen Elementpaare nur einer bestimmten Stellung fähig wären, derart, dass das positive Element immer in der einen und das negative Element immer in der anderen Kette liegt. Das ist aber nicht der Fall, und wir müssen jetzt noch berücksichtigen, dass an s Stellen positiv-negative Elementpaare gegeneinander verdreht sein werden. Wir haben seinerzeit die ν3 quergestellten Elemente auf s13 + s23 + s + δ3 Stellen verteilt, infolgedessen stossen noch an (ν3 - s13 - s23 - s - δ3) Punkten quergestellte Elemente unter sich zusammen. Unter diesen Punkten können wir die s Stellen beliebig auswählen, dementsprechend ist N1(ν1ν2ν3σ12σ23σ31) um den Faktor
zu vergrössern. An jeder dieser s Stellen tritt eine Energie e12 auf wie zwischen einem positiven und einem negativen Elementpaar.
Damit haben wir noch immer nicht alle Anordnungsmöglichkeiten berücksichtigt. Wir haben die positiv-negativen Elementpaare auf (s13 + s23 + s + δ3) Stellen verteilt. Es können bei allen positiv-negativen Elementpaaren, die an einer dieser Stellen untergebracht sind, gleichzeitig die positiven Elemente mit den negativen vertauscht werden. Diese Vertauschungen liefern, wie man leicht sieht, für die Anzahl der Anordnungsmöglichkeiten den Faktor
2 s13 + s23 + s + δ3
während sie für die Energieverhältnisse ohne Einfluss sind. Damit können wir die Zustandssumme Z1(n), soweit sie von Anordnungen herrührt, die links mit einem positiven Element beginnen, angeben. Dieselbe ist nach Gleichung (24)
Wir bilden wieder eine Funktion
Es lassen sich dann ganz entsprechend wie früher die Summationen über ν1, ν2 und ν3 ausführen. Setzt man wieder
zi = xAi / 1 - xAi
i = 1 und 2
wie oben, aber jetzt
z3 = 2xA3 / 1 - xA3(1 + B12)
so liefert die Summation über s
Hier sieht man, dass F1(x) und F1(x) formal vollständig übereinstimmen, so dass wir sofort das Endresultat der Summationen angeben können. Es ist
wobei jetzt aber
G(x) = [A1 + A2 + 2A3] - x[2A1A2(1 - B12) + A2A3(3 + B12 - 4B23) +
A3A1(3 + B12 - 4B31)] + 2x2A1A2A3[2 - B122 - 2B23 - 2B31 +
2(B12B23 + B23B31 + B31B12) - (B122 + B232 + B312)]
und
= 1 - x[A1 + A2 + A3(1 + B12)] + x2[A1A2(1 - B122) +A2A3(1 + B12 - 2B232) + A3A1(1 + B12 - 2B312)] -x3A1A2A3[1 + B12 - 2B232 - 2B312 -B122(1+B12) + 4B12B23B31] |
In genau derselben Weise wie oben finden wir schliesslich
J = m · n (d / dα) log w1
wo w1 wieder die grösste der drei Wurzeln wi bezeichnet.
Wir nehmen jetzt an
B13 = B23 = B
und
B12 = B2
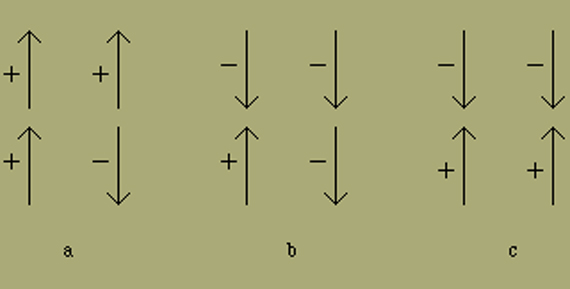
d.h. es erfordert die gleiche Energie, ob ein positives Elementpaar oder ein negatives mit einem positiv-negativen Elementpaar zusammentrifft. Wir haben in diesem Fall jeweils eine Energiestelle im ursprünglichen Sinn, wie Fig. 9a und 9b zeigt; dagegen erfordert es doppelt soviel Energie, wenn irgendwo ein positives und ein negatives Elementpaar zusammenstossen, wobei zwei Energiestellen auftreten (Fig. 9c).
Fig. 9.
Wir erinnern uns noch daran, dass wir als Nullniveau für die innere Energie den Fall gewählt haben, wo alle Elemente gleichgerichtet sind, also keine Energiestellen auftreten. Unter unseren Annahmen erhalten wir für w1 die vereinfachte Gleichung
= 1 - x[A1 + A2 + A3(1 + B2)] + x2(1 - B2)[A3(A1+A2) +(1 + B2)] - x3A3(1 - B2) |
Es ist der jetzigen Bedeutung von A1 und A2 entsprechend
A1 · A2 = 1;
A1 + A2 = 2ch2α
Setzen wir die Wechselwirkungsenergie ei zwischen benachbarten Elementen verschiedener Ketten gleich 0, d.h. A3 = 1, so erhalten wir, wie es sein muss, ein uns bekanntes Ergebnis, und zwar
und
(vgl. Gleichung 20, wo n1 = 2 zu setzen ist).
In dem anderen Grenzfall sehr starker Wechselwirkung (A3<<1) finden wir, wenn wir noch annehmen, dass auch (1 - B2) klein ist, d.h. die Wechselwirkungsenergie ei zwischen benachbarten Elementen derselben Kette ist nicht sehr gross (B = e-ei/kT)
Wir haben in der Gleichung für w1 das Glied mit x3 vernachlässigt. Wenn wir
setzen, so ergibt sich
Um recht deutlich zu sehen, wie sich die Wechselwirkung zwischen benachbarten Elementen verschiedener Ketten bemerkbar macht, lassen wir dieselbe recht gross werden, dann dürfen wir A3 = 0 setzen, wobei
Wir sehen, dass sich gegenüber dem Fall ohne Wechselwirkung (Gleichung 19) der Parameter α, d.h. das äussere Feld und die innere Energie ei um den Faktor 2 vergrössert haben.
In diesem Grenzfall lässt sich die Behandlung auch auf ein räumliches Modell ausdehnen. Haben wir nämlich n1 parallele Ketten, so haben wegen unserer Annahmen jeweils die n1 in einer Querschicht nebeneinander liegenden Elemente alle dieselbe Richtung, sodass wir jede solche Schicht jetzt als Element betrachten können, das zum Gesamtmoment den Beitrag plus oder minus n1m liefert. Damit ist der Fall auf die einfache lineare Kette zurückgeführt. Man findet danach
d.h. gegenüber Gleichung (20) eine Vergrösserung des äusseren Magnetfeldes und eine Vergrösserung der Wechselwirkungsenergie ei zwischen Elementen derselben Kette um den Faktor n1. Dieses Modell wäre praktisch stets spontan gesättigt magnetisiert. Doch wechselt die Richtung der Magnetisierung mit der des äusseren Feldes.
Nur für ein H=0 verschwindet das mittlere Moment und es lässt sich genau wie im vorigen Paragraphen zeigen, dass das Moment der wahrscheinlichsten Anordnung mit H=0 verschwindet.
§ 8.
Die lineare Kette bei Wechselwirkung
zwischen erst- und zweitbenachbarten Elementen.
Drittens untersuchen wir, wie sich unsere bisherigen Ergebnisse ändern, wenn wir annehmen, dass auch die Stellungen von zweitbenachbarten Elementen zu einander auf die Energieverhältnisse von Einfluss sind. Wir setzen wieder fest, dass in den Fällen, wo alle Elemente gleichgerichtet sind, die innere Energie verschwindet. Es erfordere die Energie ei, um von zwei nächstbenachbarten Elementen, die die gleiche Richtung haben, eines umzuklappen. Kommt es also σ mal vor, dass nächstbenachbarte Elemente entgegengesetzt gerichtet sind, und τ mal, dass zweitbenachbarte Elemente entgegengesetzt gerichtet sind, so steckt in einer solchen Anordnung die innere Energie
σei + τei'
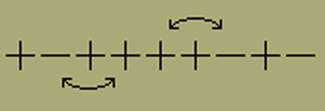
Wir fragen nun, wieviel Anordnungen von ν1 positiven und ν2 negativen Elementen diese innere Energie besitzen. Wir beschränken uns zunächst wieder auf die Anordnungen, deren erstes Element links positiv ist. Um die Anordnungsmöglichkeiten bequem ablesen zu können, lassen wir eine gewünschte Anordnung in der folgenden Weise allmählich entstehen. Wir bilden uns zunächst eine Kette, die mit einem positiven Element links beginnend abwechselnd aus einem positiven und einem negativen Element besteht. In dieser Kette sollen bereits alle σ=2s+δ Energiewerte ei auftreten. Diese Kette enthält dann (s+1) positive und (s+δ) negative Elemente. Die Kette ende rechts mit einem positiven oder negativen Element, je nachdem, ob δ=0 oder δ=1 ist. Bringt man im Innern dieser Kette an einer Stelle weitere Elemente, positive oder negative, [unter,] so kommt es jetzt wie Fig. 10 zeigt, zweimal vor, dass zweitbenachbarte Elemente entgegengesetzt gerichtet sind.
Fig. 10.
Bringen wir also die noch nicht verteilten (ν1-s-1) positiven und (ν2-s-δ) negativen Elemente an r1 bzw. r2 Stellen im Innern der Kette unter, so tritt dabei 2(r1+r2) mal die Energie ei' auf. Die r1 und r2 Punkte, wo wir die Elemente einfügen, lassen sich, wie man leicht sieht, auf
Weisen auswählen. Wir führen noch die Grössen ε1, ε1' und ε2 ein, die die Werte 1 oder 0 annehmen, je nachdem wir am linken bzw. rechten Ende der Kette positive bzw. negative Elemente unterbringen oder nicht. Danach haben wir die (ν1-s-1) positiven auf (r1+ε1+ε1'(1-δ)) und die (ν2-s-δ) negativen Elemente auf (r2+ε2δ) Stellen zu verteilen. Das geht nach Gleichung (10) auf
Arten.
Ist eine der Grössen ε1, ε1'(1-δ) und ε2δ gleich 1, so kommt es ein weiteres Mal vor, dass zwei zweitbenachbarte Elemente entgegengesetzt gerichtet sind, so dass
τ = 2(r1 + r2) + ε1 + ε1'(1-δ) + ε2δ
Die Ermittlung der Zustandssumme
(es ist über s, r1 und r2 von 0 bis unendlich, über ν1+ν2=n und über δ, ε1, ε1', ε2 von 0 bis 1 zu summieren) erfolgt in ganz analoger Weise wie in den früher betrachteten Fällen. Wir wollen sie daher nur kurz andeuten. Es ist wie früher zur Abkürzung gesetzt
(14) |
A1 = eα,A2 = e-α,B = e-ei / kT |
und ausserdem jetzt
E = e-ei' / kT
Man betrachtet wieder
Setzt man vorübergehend
zi = xAi / 1 - xAi
so liefert die Summation über ν1 und ν2
Jetzt lassen sich die Summationen über r1 und r2 ausführen. Man erhält
Nun ist die Summation über s auszuführen und dann sind für δ, ε1, ε1' und ε2 die Werte 0 und 1 einzusetzen. Durch Vertauschen der Indizes 1 und 2 erhält man den Ausdruck F2(x), der den Anordnungen entspricht, die links mit einem negativen Element beginnen. Man erhält schliesslich
Für das mittlere Moment kommt nur die grösste unter den Wurzeln wi in Betracht, die wir mit w1 bezeichnen und die aus der Gleichung
zu bestimmen ist. Man findet
wi = chα + W
wo
und weiter
J = m · n (d / dα) log w1
Da im Allgemeinen die Energie ei', die erforderlich ist, um von 2 zweitbenachbarten Elementen das eine umzuklappen, klein sein wird, so ist E = e-ei / kT ungefähr gleich 1, sodass wir die Glieder mit (E2 - 1)2 vernachlässigen dürfen. Dann sieht man aber, dass sich die Wechselwirkung zwischen zweitbenachbarten Elementen bemerkbar macht, wie eine Vergrösserung der Wechselwirkung zwischen nächstbenachbarten Elementen, denn an die Stelle von B2 = e-2ei / kT in Gleichung (19) ist jetzt B2E2 < B2getreten. Das entspricht einer Vergrösserung von ei.
Wir stellen auch hier wieder wie im Paragraphen 6c) für den Fall H = 0 die Gleichungen zur Bestimmung der Maximalwahrscheinlichkeit auf. Dieselben lauten:
Die Gleichung a) können wir auch in der Form
schreiben. Die Division von c) und d) ergibt
oder r1 = r2 und weiter
ν1 = ν2