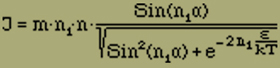BIBLIOTHECA AUGUSTANA
Ernst Ising
1900 - 1998
Contribution to theTheory of Ferromagnetism
1925
|
|||
|
______________________________________________________________________________
|
|||
3. The three-dimensional model
Also, one does not arrive at a different result using a three-dimensional model which agrees with the assumptions above. We can show without difficulty the result in an idealized border case. We imagine the three-dimensional ferromagnetic crystal constructed of n1 regularly arranged chains, as we considered above. Again, each element can only take the two orientations in which its moment points in the extension direction of its chain. However, the portions of the moment perpendicular to it require too much energy to be realized. This supposition can only be favorable for the intensity of magnetization in the direction along the chain considered by us. 1) We determine again that the inner energy disappears when all elements are similarly oriented. If at one position within the crystal similar poles of neighboring elements of the same chain collide, then the crystal shall have the energy ε as before. In addition, each time when somewhere two elements of neighboring chains lying next to each other are oppositely oriented, it should contain the energy ε. In our idealized border case, the energy ε should be so large that two neighboring elements lying next to each other are never oppositely oriented, i.e. however, that only a tiltover of the elements in layers occurs. Practically, we deal again with a simple linear chain whose elements are now these layers. Consequently, we have to replace in the former calculations
m by n1 · m
and
ε by n1ε
Therefore we find in our border case
Although here we expect to find a more favorable result than from a general three-dimensional model, we recognize here too a disappearance of J with H.Thus in the model chosen here, whose essential characteristic is the restriction of the mutual effect on the one between neighboring elements, no ferromagnetism appears. Nevertheless, the present research should be of some interest for the problem of ferromagnetism because, with the assumption of very slowly decreasing (electrical) reciprocal efficiency interaction, one arrives at the great difficulty that considerable electrical field intensities should exist in an electrical conductor.
I should like to thank Prof. Dr. W. Lenz for suggesting this work and the interest he has shown in it.
Hamburg, December 8, 1924
|
|||