| |
|
- Ὀ σ τ ο μ ά χ ι ο ν
ἀπόσπασμα
Textus:
Archimedis opera omnia,
vol. 2, p. 420 sqq.
ed. J. L. Heiberg,
Lipsiae 1881/1915
- ________________________________________
- Hoc fragmentum arabice servatum est in codd. Berolin. Mf. 258 et Mq 559, Bodleian. 960, codiceque quodam Instituti rerum Indiae Londinensis. Henricus Suter e codd. Berloninensibus textum edidit et germanice interpretatus est (Abhandlungen zur Geschichte der Mathematik IX (1899) p.491 sqq.).
Das Buch des Archimedes
über die Teilung der Figur Stomaschion
in vierzehn zu ihr in Verhältnis
stehende Figuren.
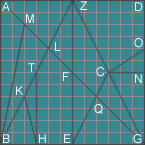
Wir zeichnen ein Parallelogramm, es sei dies ABGD, halbieren BG in E, errichten EZ senkrecht auf BG, ziehen die Diagonalen AG, BZ und ZG, halbieren ebenfalls BE in H, und errichten HT senkrecht auf BE ; dann legen wir das Lineal an den Punkt H und visieren nach dem Punkt A und ziehen HK, halbieren AL in M und ziehen BM. so ist das Rechteck AE in sieben Teile geteilt. Hierauf halbieren wir GD in N, ebenso ZG in C, ziehen EC, legen das Lineal an die Punkte B und C an und ziehen CO, ziehen noch CN, so ist auch das Rechteck ZG in sieben Teile, aber auf andere Weise als das erste, geteilt, mithin das ganze Quadrat in vierzehn Teile.
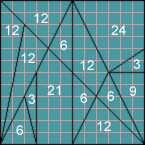
Wir beweisen nun, dass jeder der vierzehn Teile zum ganzen Quadrat in rationalem Verhältnis stehe.
Weil ZG die Diagonale des Rechtecks ZG ist, so
ist Dreieck DZG die Hälfte dieses Rechtecks, also 1/4 des Quadrates. Aber Dreieck GNC ist 1/4 von Dreieck DZG, weil, wenn wir EC verlängern, es in den Punkt D trifft, und dann also Dreieck GDC die Hälfte des Dreiecks DZG und gleich den beiden Dreiecken GNC und DNC zusammen ist; also ist Dreieck GNC = 1/16 des Quadrats. Wenn wir nun ferner annehmen, die Linie OC sei nach dem Punkte B gerichtet, wie sie in der Tat auch gezeichnet wurde, so ist die Linie NC parallel zur Seite BG des Quadrates, resp. des Dreiecks OBG, also hat man die Proportion
BG : NC = GO : NO.
Es ist aber BG das Vierfache von NC, also auch GO das Vierfache von NO; deshalb ist nun GN das Dreifache von NO, und Dreieck GNC = 3 ONC. Da aber, wie wir gezeigt haben, Dreieck GNC =1/16 des Quadrates ist, so ist Dreieck ONC = 1/48 des Quadrates. Weil ferner Dreieck GDZ =1/4 des Quadrates ist und deshalb GNC =1/16 desselben und Dreieck NCO = 1/48 desselben, so bleibt für das Viereck DOCZ = 1/6 der Quadratfläche übrig. Nach der Voraussetzung geht ferner die Linie NC durch den Punkt F, und es wäre CF parallel zu GE; also hat man die Proportion EG : CF = EQ : CQ = GQ : FQ. Weil nun EQ = 2 CQ und GQ = 2 FQ, so ist Dreieck EQG das Doppelte jedes der beiden Dreiecke GCQ und EFQ. Es ist aber klar, dass Dreieck EGZ = 2 mal Dreieck EFG ist, weil ZE = 2FE ist. Das Dreieck EGZ ist aber = 1/4 des Quadrates, also Dreieck EFG = 1/8 desselben. Dieses ist aber das Dreifache jedes der beiden Dreiecke EFQ und GCQ; also ist jedes dieser beiden Dreiecke = 1/24 des Quadrates AG. Und das Dreieck EGQ ist das Doppelte jedes der beiden Dreiecke EFQ und GCQ; also ist es = 1/12 des Quadrates. Weil ferner ZF = EF ist, so ist Dreieck ZFG = Dreieck EFG; wenn wir nun Dreieck GCQ = Dreieck EFQ wegnehmen, so bleibt Viereck FQCZ = Dreieck EGQ; also ist auch Viereck FQCZ =1/12 des Quadrates AG.
Wir haben nun das Rechteck ZG In 7 Teile geteilt und gehen nun zur Teilung des andern Rechtecks
über.
Weil BZ und EC zwei parallele Diagonalen sind, und ZF = EF ist, so ist Dreieck ZLF = EFQ, mithin Dreieck ZLF = 1/24 des Quadrates AG. Weil BH = HE ist, so ist Dreieck BEZ das Vierfache des Dreiecks BHT; denn jedes desselben ist rechtwinklig. Da aber Dreieck BEZ = 1/4 des Quadrates ABGD ist, so ist Dreieck BHT = 1/16 desselben. Nach unserer Voraussetzung geht ferner die Linie HK durch den Punkt A; also hat man die Proportion
AB : HT = BK : KT.
Es ist aber AB = 2 HT, also auch BK = 2 KT, mithin BT = 3 KT ; also ist Dreieck BHT das Dreifache des Dreiecks KHT. Weil aber Dreieck BHT = 1/16 des ganzen Quadrates ist, so ist Dreieck KHT = 1/48 desselben. Ferner ist Dreieck BKH das Doppelte des Dreiecks KHT, also = 1/24 des Quadrates. Da weiter BL =2 ZL, und AL = 2 LF ist, so ist Dreieck ABL das Doppelte des Dreiecks ALZ und Dreieck ALZ das Doppelte des Dreiecks ZLF. Weil aber Dreieck ZLF = 1/24 des ganzen Quadrates ist, so ist Dreieck ALZ == 1/12 desselben, also Dreieck ABL = 1/6. Es ist aber Dreieck ABM = Dreieck BML, also jedes dieser beiden Dreiecke = 1/12 des Quadrates. Es bleibt noch übrig das Fünfeck LFEHT = der Hälfte eines Sechstels mehr der Hälfte eines Achtels des ganzen Quadrates.
Wir haben also auch das Quadrat AE in 7 Teile geteilt; mithin ist die ganze Figur ABGD in 14 Teile geteilt, welche zu ihr in Verhältnis stehen; und das ist, was wir wollten.
|
|