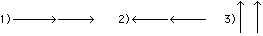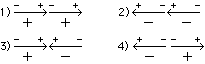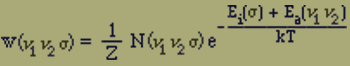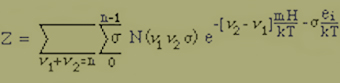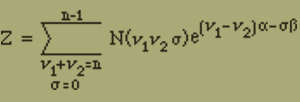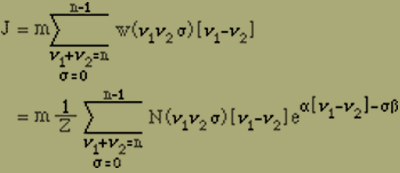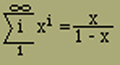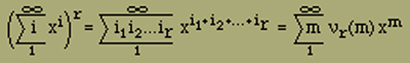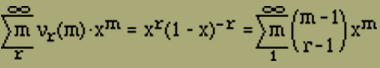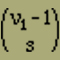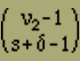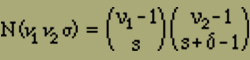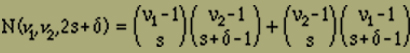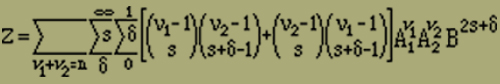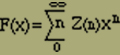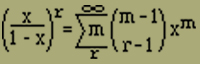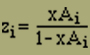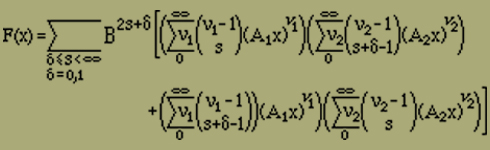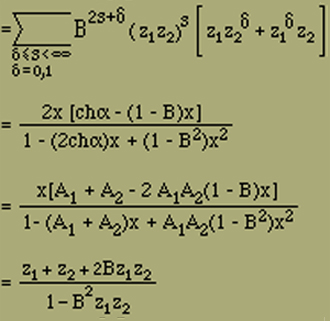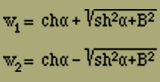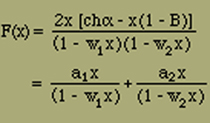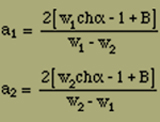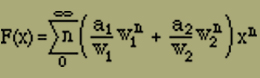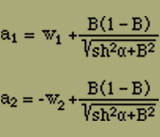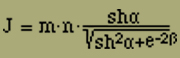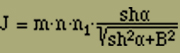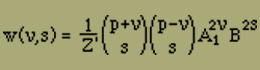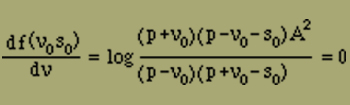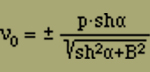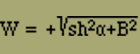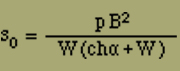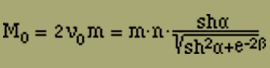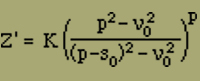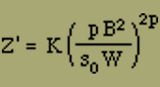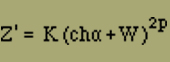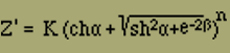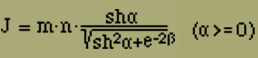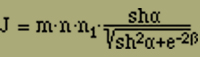BIBLIOTHECA AUGUSTANA
Ernst Ising
1900 - 1998
Beitrag zur Theorie desFerro- und Paramagnetismus
1924
|
|||||||||||||||||||||||||||||
|
____________________________________________________________
|
|||||||||||||||||||||||||||||
Hauptteil
I.Das mittlere magnetische Momentder einfachen linearen Ketteund verwandter Modelle.
――――――――――
§ 1.Annahmen.
Wir denken uns einen Ferromagneten aus regelmässig angeordneten Elementarmagneten (magnetischen Dipolen) aufgebaut. Diese Elementarmagnete, die wir kurz Elemente nennen wollen, sollen nur wenige der Kristallsymmetrie entsprechende, energetisch ausgezeichnete Lagen einnehmen. Mit jeder Lage soll auch die entgegengesetzte möglich sein. Diese Annahmen sind durch die oben erwähnten Beobachtungen von Weiss an Pyrrhotin und Magnetit und die Vorstellung der Quantentheorie nahegelegt. Die Elemente gehen infolge der Wärmeagitation von einer möglichen Lage in eine andere über. Dass solche Umklapperscheinungen im festen Körper überhaupt stattfinden, wird verständlich, wenn man an die, bei der Fremd- und Selbstdiffusion beobachteten Tatsache des Platzwechsels der Atome denkt.Ausser von einem angelegten äusseren Magnetfeld sollen die Elemente noch durch die Kräfte beeinflusst werden, die sie gegenseitig auf einander ausüben. Ueber diese Kräfte, die etwa elektrischer Natur sein mögen (Vgl. W. Schottky, Phys. Zeitschr. 23. 448. 1922.), können wir keine näheren Angaben machen; wir nehmen jedoch an, dass sie mit der Entfernung rasch abklingen, so dass wir im Allgemeinen in erster Näherung nur die Wirkung benachbarter Elemente zu berücksichtigen brauchen. Die letztere Annahme steht in einem gewissen Gegensatz zur Hypothese des molekularen Feldes, von dem P. Weiss (C. R. 157. 1405. 1913. und C. R. 158. 29. 1914.) gezeigt hat, dass es nicht magnetischer Natur sein kann. Wir setzen an, dass unter allen möglichen Stellungen, die zwei benachbarte Atome zu einander einnehmen können, diejenigen die geringste Energie erfordern, bei denen beide gleichgerichtet sind. (Fig. 1.)
|
|||||||||||||||||||||||||||||
(5) |
Die Grösse Z, die sogenannte Zustandssumme, bestimmt sich aus der Beziehung
Wir finden, wenn wir für E und Ea die Werte aus Gleichung (1) und (3) einsetzen,
Führen wir die Abkürzungen
(6) α = (mH) / kT
und
(7) β = ei / kT
ein, so ist
(8) |
Indem man jedes Moment
(2) M = m(ν1 - ν2)
mit der Wahrscheinlichkeit w(ν1,ν2,σ) multipliziert und über alle zulässigen Werte von ν1, ν2 und σ summiert, erhält man das mittlere Moment oder die Intensität der Magnetisierung
oder wegen der Definition von Z (Gleichung 8)
(9) J = m (d / dα) log Z
§ 3.
Berechnung der Zahl der Anordnungsmöglichkeiten.
Die Bestimmung der Grössen N(ν1,ν2,σ) lässt sich leicht durchführen, wenn man weiss, wie oft sich eine Zahl m als Summe von r ganzen Zahlen >=1 darstellen lässt, wobei verschiedene Anordnungen der Summanden als verschiedene Darstellungen zu zählen sind. Wir beantworten daher zunächst diese Frage.
Multipliziert man die Reihe
r mal mit sich selbst
so setzt sich in dem Produkt jeder Exponentadditiv aus r ganzen Zahlen >=1 zusammen und zwar kommt jede denkbare Summe aus r solchen Zahlen im eingangs definierten Sinne genau einmal vor. Wenn wir nun alle Glieder, die denselben Exponenten m haben, zusammenfassen, so gibt der Koeffizient dieses Gliedes νr(m) an, wie oft sich m als Summe von r ganzen Zahlen >=1 darstellen lässt. Man findet
(10) |
denn nach dem binomischen Satz
(11) |
Es erweist sich als zweckmässig, die in der Anzahl N(ν1,ν2,σ) zusammengefassten Anordnungen in zwei Gruppen einzuteilen, und zwar je nachdem, ob die Anordnung an dem einen Ende der Kette, sagen wir etwa an dem linken, mit einem positiven Element beginnt oder mit einem negativen. Um die Anzahl N1(ν1,ν2,σ) der Anordnungen, deren erstes Element links positiv ist, zu finden, lassen wir eine solche Anordnung in der folgenden Weise entstehen.
Die positiven Elemente seien zunächst lückenlos in einer Reihe angeordnet. In dieser Kette markieren wir uns in beliebiger Weise s Punkte (s < ν1), an denen die Reihe zur Einfügung von negativen Elementen in noch zu erörternder Zahl auseinander geschoben werden soll. Denkt man sich an einer dieser Stellen negative Elemente eingeschoben, so entstehen, wie Fig. 4 zeigt, zwei Energiestellen.
Fig. 4.
Man hat also an jedem der s Punkte zwei Energiestellen unterzubringen. Wir führen eine Grösse δ ein, die die Werte 1 und 0 annimmt, je nachdem, ob wir am rechten Rand der Kette negative Elemente anfügen werden oder nicht. Ist δ=1, so müssen wir rechts vom äussersten positiven Element eine weitere Energiestelle anbringen. Bei beliebiger Verteilung der ν2 negativen Elemente auf die (s+δ) Stellen erhält man Anordnungen, die alle dieselbe innere Energie
σei = (2s+δ)ei, δ=0 oder 1
und dasselbe Moment m(ν1-ν2) und damit auch dieselbe äussere Energie besitzen, und deren erstes Element links positiv ist. Wenn man daher die sich so ergebenden Möglichkeiten abzählt, erhält man die gesuchte Zahl N1(ν1,ν2,σ).
Hierzu ist erforderlich, die Anzahl der Möglichkeiten zu kennen
a) zur Unterbringung der s Paare von Energiestellen zwischen den positiven Elementen und
b) zur Verteilung der ν2 negativen Elemente auf die durch die Energiestellen geöffneten (s+δ) Lücken. Nun lassen sich (a) die s Plätze für die Energiestellenpaare auf
verschiedene Weisen auswählen. Sodann kann man (b) ν2 nach Gleichung (10) auf
Arten als Summe von (s+δ) Zahlen darstellen. Jede Aufteilung der negativen Elemente in (s+δ) Portionen ist ja eine solche Darstellung von ν2 als Summe von (s+δ) Zahlen. Da wir bei jeder Verteilung der Energiestellen die negativen Elemente noch in beliebiger Weise in den Lücken unterbringen dürfen, so ist
(12) |
wobei
σ=2s+δ und δ=0 oder 1 ist.
Die übrigen links mit einem negativen Element beginnenden Anordnungen erhält man durch Vertauschen der negativen und positiven Elemente beim obigen Verfahren; ihre Anzahl N2(ν1,ν2,σ) ergibt sich daher, wenn man in Gleichung (12) ν1 und ν2 vertauscht. Durch Addition von N1 und N2 erhält man schliesslich
(13) |
§ 4.
Ausführung der Summation.
a) Exakte Summation.
Nachdem wir somit alle Anordnungsmöglichkeiten nach ihrem Moment und ihrer Energie sortiert und abgezählt haben, können wir uns der Berechnung des mittleren Momentes J zuwenden. Dabei handelt es sich im Wesentlichen um die Bestimmung der Zustandssumme Z, wie Gleichung (9) zeigt. Es ist wegen Gleichung (8) und (13), wenn wir aus formalen Gründen vorübergehend
(14) A1 = eα, A2 = e-α und B = e-β
setzen,
(15) |
Wir haben nur die Nebenbedingung
(4) ν1 + ν2 = n
zu berücksichtigen, dagegen dürfen wir über s beliebig weit summieren, da unser Ausdruck für zu grosse Werte von s wegen der bekannten Eigenschaft der Binomialkoeffizienten von selbst verschwinden.
In sehr einfacher Weise, die sich leicht auf kompliziertere Fälle übertragen lässt, gelingt die Summation, wenn man Z als Funktion von n auffasst und zunächst
(16) |
betrachtet, wobei x eine beliebige hinreichende Variable ist. Wir hoffen dabei, F(x) in geschlossener Form darstellen zu können und rückwärts Z(n) durch Entwicklung nach Potenzen von x in summierter Form zu erhalten. Diese Methode beseitigt die störende Nebenbedingung ν1+ν2=n, da wir die Summation über n in Gleichung (16) dadurch ausführen können, dass wir über ν1 und ν2 unabhängig von einander von 0 bis unendlich summieren. Diese beiden Summationen lassen sich mit Hilfe von Gleichung
(11) |
ausführen. Danach ist, wenn wir vorübergehend
(i = 1 oder 2) |
einführen
denn A1+A2 = 2chα und A1A2 = 1 (Gleichung 14).
Damit ist bereits F(x) in geschlossener Form gewonnen. Um nun Z(n) zu erhalten, nehmen wir eine Partialbruchzerlegung von F(x) vor und entwickeln jeden Bruch nach Potenzen von x. Wenn wir hierzu w1 und w2 aus der Gleichung
(1 - w1x)(1 - w2x) = 1 - (2chα)x + (1 - B2)x2
bestimmen, so ergibt sich
(17) |
und es ist
a1 und a2 bestimmen sich zu:
Die Entwicklung von F(x) nach Potenzen von x ergibt
und wegen Gleichung (16)
(18) Z(n) = (a1 / w1)w1n + (a2 / w2)w2n
Da n eine sehr grosse Zahl ist (Grössenordnung 108), so dürfen wir in Gleichung (18) das Glied a2w2n-1 neben dem ersten Glied vernachlässigen, denn es ist immer w1 > 1 und w2 < 1 (Gleichung 17), wenn wir nur von dem Fall unendlich grosser Wechselwirkung bei verschwindendem äusserem Feld (B = 0, α = 0) absehen. Man findet weiter durch eine einfache Rechnung
daraus sieht man, dass
1 <= a1/w1 <= 2
und dass a1/w1 mit wachsendem α monoton abnimmt und infolgedessen bei der logarithmischen Ableitung von Z nach α einen zu vernachlässigenden Beitrag liefert. Somit finden wir für die Intensität der Magnetisierung (Gleichung 9)
J = m · (d / dα) log Z = m · n · (d / dα) log w1
(19) |
Haben wir nicht eine, sondern zwei Ketten der oben beschriebenen Art, so haben wir, um alle Anordnungsmöglichkeiten zu erhalten, jeden Zustand der einen Kette mit jedem Zustand der anderen zu kombinieren, d.h. die Zustandssumme ist in diesem Fall
Es ist dabei angenommen, dass sich die Elemente verschiedener Ketten nicht beeinflussen. Haben wir n1 solche parallele Ketten, so finden wir entsprechen für die Zustandssumme
Zn1 = Zn1
und infolgedessen für das mittlere Moment
(20) |
b) Näherungsmethode.
Mit verschwindendem äusseren Feld (α = (mH / kT) = 0) verschwindet auch das mittlere Moment J, wir haben also keine Hysteresiserscheinung. Dieses Ergebnis ist bei unserem Ansatz ganz selbstverständlich. Zu jeder Stellung kommt diejenige vor, bei der alle Elemente entgegengesetzt gerichtet sind, und die somit das entgegengesetzt gleiche Moment hat. Diese beiden Anordnungen erfordern für H = 0 dieselbe Energie, sodass sich im Mittel kein Moment ergeben kann, da sich die Momente der verschiedenen Stellungen paarweise aufheben. Das unerwünschte Ergebnis
J = 0 für H = 0
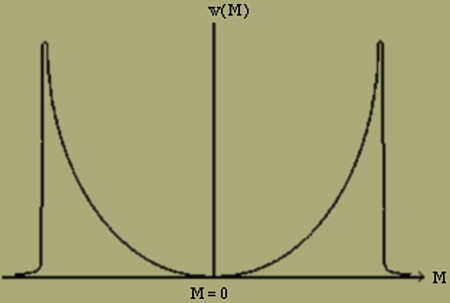
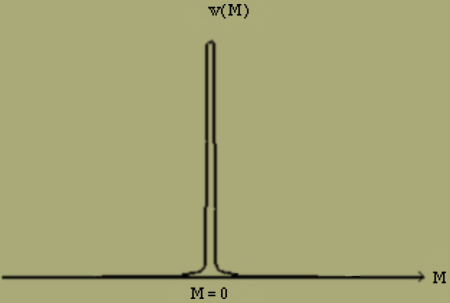
scheint also nur eine Folge der statistischen Mittelbildung über alle möglichen Lagen zu sein, und man kann daran denken, es dadurch zu beseitigen, dass man etwa die Anordnungen mit positivem und die mit negativem Moment zunächst gesondert betrachtet. Die Wahrscheinlichkeit w(ν1,σ2,ν) ist eine Funktion der Momente M und der Anzahl σ der Energiestellen. Wir denken uns für den Fall H = 0 zu jedem festen M den jeweils grössten Wert von w(ν1,ν2,σ) ermittelt und die so gefundenen Grössen als Funktion von M aufgetragen. Wir erhalten so eine gerade Funktion von M, da für H = 0 die positive und die negative Richtung nicht vor einander ausgezeichnet sind. Diese Funktion kann nun entweder zwei gleiche symmetrisch zu M=0 gelegene Maxima haben (Fig. 5)
Fig. 5.
oder nur ein einziges, und zwar aus Symmetriegründen bei M=0 (Fig. 6).
Fig. 6.
In beiden Fällen ergibt sich bei der statistischen Mittelbildung für die Intensität der Magnetisierung J = 0, was jedoch, falls die Wahrscheinlichkeit zwei Maxima hat, (Fig. 5), keineswegs dem wirklichen physikalischen Verhalten entspricht. In diesem Falle schwankt das Moment um einen der beiden Werte, zu dem ein Maximum von w gehört, und es ist sehr unwahrscheinlich, dass das Moment von selbst einmal auch bei langer Beobachtungszeit in den anderen Wert übergeht, dem das zweite Maximum von w entspricht. Es liegt dann eben kein thermischer Gleichgewichtszustand, sondern nur ein Zustand maximaler Wahrscheinlichkeit vor.
Um zu entscheiden, welche von den beiden angegebenen Möglichkeiten vorliegt, führen wir jetzt eine zweite Berechnung von J durch. Zur Vereinfachung setzen wir
ν1 - 1 = p + ν
ν2 - 1 = p - ν
wo jetzt ν von -p nach +p läuft. Dann ist
n = ν1 + ν2 = 2(p - 1)
also p die halbe Anzahl der Elemente der Kette. Ferner ist jetzt das Moment einer Anordnung
M = m(ν1 - ν2) = 2ν · m
Wir nehmen noch an, dass p + ν1, p - ν und s gross gegen 1 sind, was das Resultat rechtfertigen wird. Dann können wir die verschiedenen Terme, aus denen sich w(ν,s) zusammensetzt (Gleichung 5 und 13), als gleich betrachten und schreiben
Ausserdem dürfen wir dann ν und s als stetige Variable auffasen und die Fakultäten in den Binomialkoeffizienten mit Hilfe der Stirlingschen Formel umformen. Es ist dann
w(ν, s) = 1/Z' · ef(ν,s)
wo
f(ν,s) = (p+ν)lg(p+ν) + (p-ν)lg(p-ν) - (p+ν-s)lg(p+v-s) - (p-ν-s)lg(p-ν-s) -
2slgs + νlgA12 + slgB2
In ganz analoger Weise wie früher haben wir (vgl. Gleichung 15 und 9)
(15a) |
(9a) J = m (d / dα) log Z'
Wir wollen jetzt zunächst die Maxima von w(ν,s) aufsuchen. Bezeichnen wir durch den Index 0 die Koordinaten, denen die Maxima von w entsprechen, so haben wir für dieses folgende Gleichungen:
(21)
a)
oder
a')
p2 - ν02 = s0[p+ν0cotghα]
und
b)
df(ν0,s0)/ds = log(p+ν0-s0)(p-ν0-s0)B2/s02 = 0
oder
b')
(p-s0)2-ν02 = s02B-2
b'')
p2-ν02 = s0[2p+s0(B-2-1)]
Aus (a') und (b') ergibt sich
s0 = B2/1-B2 · [ν0cotghα-p]
Diesen Wert von s0 setzen wir in (a') ein, dann finden wir
(p2-ν02)(1-B2) = B2[ν02cotgh2α-p2]
oder
p2 = ν0(1+(B2/sh2α))
oder
Setzen wir zur Abkürzung vorübergehend
so ist, wenn wir noch den Wert für ν0 in die Gleichung für s0 einführen
Da aber die Anzahl der Energiestellen nicht negativ sein kann, so ist nur das Pluszeichen zulässig. Die Wahrscheinlichkeit w(ν,s) hat also immer nur ein einziges Maximum und zwar bei
(22)
a)
ν0 = p · shα/W
b)
Diesem wahrscheinlichsten Zustand entspricht das Moment
(23)
Wir sehen, dass M0 mit dem mittleren Moment J (Gleichung 19) zusammenfällt.
Man bestätigt leicht, dass wir es bei (ν0,s0) wirklich mit einem Maximum zu tun haben, indem man zeigt, dass
d2f(ν0,s0)/dν2 < 0
und dass
fνν · fss - fνs2 = 4p2/(p2-ν02) > 0
Führen wir zunächst die zweite Berechnung von J zu Ende, so haben wir Z' zu ermitteln. Dazu entwickeln wir f(ν,s) an der Stelle des Maximums (ν0,s0) in eine semikonvergente Reihe, die wir mit den quadratischen Gliedern abbrechen. Nach Gleichung (15a) findet man
Z' = ef(ν0,s0) · K
wo zur Abkürzung gesetzt ist
Von diesem Faktor K lässt sich leicht zeigen, daß er kleiner als π ist und mit wachsendem α monoton abnimmt; infolgedessen werden wir den Betrag, den K bei der logarithmischen Ableitung von Z' liefert, vernachlässigen dürfen. Unter Berücksichtigung der Gleichungen (21a) und (21b) findet man
Mittels Gleichung (21b', 22a) erhält man weiter
Setzt man für s0 den Wert aus Gleichung (22b) ein, so ergibt sich
oder
da 2p = n und
Für die Intensität der Magnetisierung finden wir dann nach Gleichung (9a) unter Berücksichtigung des oben über den Faktor K Gesagten
(19)
also dasselbe Ergebnis, das uns bereits die erste Rechnung geliefert hatte.
§ 5.
Diskussion des Ergebnisses.
Die zweite Berechnung von J zeigt uns jedoch, dass der tiefere Grund für das Verschwinden des mittleren Moments mit dem äusseren Feld nicht darin besteht, dass sich, wie wir es am Anfang des vorigen Paragraphen annahmen, die Momente paarweise zerstören, sondern dass dies Verhalten in ganz anderer Weise durch unseren Ansatz bedingt ist. Ist die Anzahl n der Elemente sehr gross - eine Voraussetzung, die der zweiten Rechnung zugrunde lag -, so ist das mittlere Moment J von der wahrscheinlichsten Anordnung ganz allein bestimmt, was ja darin zum Ausdruck kommt, dass wir bei der Ermittlung von J den Beitrag des Faktors K vernachlässigen durften. Für die Maximalwahrscheinlichkeit ist es aber ohne Einfluss, wenn wir den Bereich der zur Konkurrenz zugelassenen Anordnungen einschränken, wofern wir nicht gerade die wahrscheinlichsten Anordnungen selbst ausschliessen. Aus dieser Bemerkung folgt aber, dass, wenn wir für H >= 0 nur die Anordnung betrachten, deren Moment M >= 0 ist, dass dann für das mittlere Moment immer noch gilt
also
J = 0 für H = 0
Letzteres gilt natürlich nur bis auf einen zu vernachlässigenden Fehler, der um so kleiner ist, je grösser n ist. Das Verschwinden von J mit H ist also wesentlich dadurch bedingt, dass die Komplexionszahl der Anordnungen mit dem Moment Null sehr viel grösser ist, als die für die Anordnung mit irgend einem anderen Moment. Hieraus folgt aber, dass es unmöglich ist, unter den gemachten Annahmen zu einer vollständigen Erklärung des Ferromagnetismus zu gelangen.
Wir gehen jetzt dazu über, den Verlauf der Anhängigkeit der Magnetisierungsintensität J vom äusseren Feld H, der inneren Energie ei und der Temperatur, wie er uns durch Gleichung (19) gegeben ist, für H nicht gleich 0 zu untersuchen. Wir betrachten zunächst den Fall
β = ei / kT = 0
Hier haben wir reinen Paramagnetismus. Das jeweilige Verhältnis von der Magnetisierungsintensität zur Sättigungsintensität
J0 = n · m
ist dann einfach
|J| / |J0| = tgh α
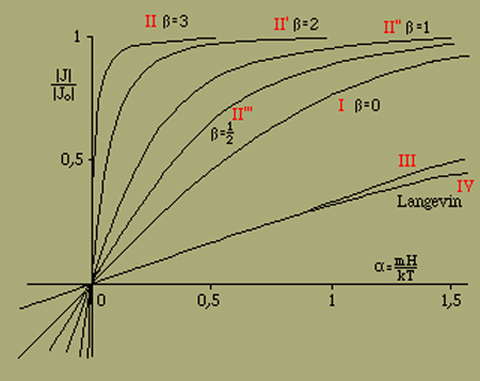
wie wir es in der Kurve I der Fig. 7 dargestellt haben.
Fig. 7.
Diese steigt bekanntlich für kleine α geradlinig an, wir haben also eine Proportionalität zwischen J und α.
J wächst linear mit H und 1/T; das Curiesche Gesetz ist also erfüllt. Für hinreichend kleine α haben wir für das mittlere Moment pro Atom, falls wir annehmen, dass H in die positive Richtung weist.
|m| = (|m|2 · H) /kT
Für große Werte von α nähert sich die Kurve asymptotisch dem Wert 1, doch lassen sich praktisch die dazu notwendigen magnetischen Felder nicht realisieren. Die grössten Werte, die α annehmen kann, liegen etwa bei 1,5. Dabei nehmen wir an, dass
H = 5 · 104 Gauss
T = 10° - 20° (absolut)
m = 6 Bohrsche Magnetonen
~ 6 · 10-20 E.G.S.
Wir lassen jetzt die Wechselwirkungsenergie ei zwischen den Elementen anwachsen. Wir erhalten dabei zunächst ganz ähnliche Kurven wie oben, nur steigen sie steiler an und nähern sich eher dem Wert I, und zwar gilt [dies] um so mehr, je grösser ei ist. Die Sättigungsintensität wird also, wie dies zu erwarten war, um so eher und besser erreicht, je stärker sich die Elemente beeinflussen. Solange α < e-β ist, findet man für das mittlere Moment pro Element
|m| = ((|m|2 · H) /kT) · eei/kT
Für α > e-β schreibt man dagegen zweckmässig
In der Grenze sehr starker Wechselwirkung (ferromagnetischer Fall) ist
|J| / |J0| = +- 1
je nachdem ob H > 0 oder H < 0 ist.
Fig. 7.
In der Kurve II der Fig. 7 ist
β = ei/kT = 3
gesetzt; dabei halten wir uns an die Angabe von W. Schottky, der in der oben zitierten Arbeit für die Umpolung eines Atoms im Kristall eine Energie von der Grössenordnung
3 - 6 · 10-13 Erg
entsprechend einigen tausend Grad berechnet.
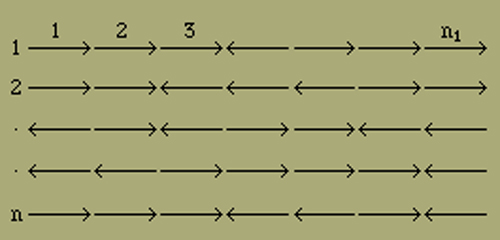
Zum Schluss dieses Abschnittes sei noch ein idealisierter Grenzfall eines flächenhaften Modells erwähnt. Die Elemente seien in einer Ebene in parallelen Ketten angeordnet und es enthalte jede Kette n Elemente. Jedes Element kann wie früher die beiden Stellungen einnehmen, bei denen sein magnetisches Dipolmoment in die Anordnungsrichtung seiner Kette fällt. Es sollen aber jetzt die Elemente innerhalb einer Kette überhaupt nicht aufeinander wirken, dagegen erfordere es die Energie ei, wenn in zwei benachbarten Ketten von zwei gleichgerichteten Elementen eines umgeklappt wird, jedoch nur, wenn die beiden Elemente unmittelbar nebeneinander liegen.
Fig. 8.
Es ist zweckmässig, bei diesem in Fig. 8 angedeuteten Modell die Anordnung der Elemente in anderer Weise aufzufassen; man kann nämlich sagen, die Elemente sind in n1 Querreihen angeordnet, von denen jede n nebeneinander liegende Elemente enthält. Von einer solchen Querreihe gilt aber, abgesehen von dem garnicht in Betracht kommenden Umstand, dass die Richtung des äusseren Feldes und der Dipolmomente jetzt normal zur Anordnungsrichtung der Elemente liegt, genau dasselbe, was wir oben über die einfache Kette gesagt haben. Daraus folgt für das mittlere Moment unseres Modells