Effizienzberechnung
oder "Wie weit komme ich bei welchem Wind?"
Hintergrund
Fragt man einen Aviation-Laien wie viel länger ein Flugzeug braucht für einen Flug bei konstantem airspeed mit Hin- und Rückflug, wobei der Hinflug mit Rückenwind und der Rückflug mit Gegenwind gleicher stärke erfolgt, so ist ein Großteil der Meinung, dass sich die Winde ausgleichen. Die Flugzeit wäre so unabhängig von der Windgeschwindigkeit. Dieser Irrglaube verpufft schnell, wenn man die Frage in den Raum stellt, ob das auch gilt, wenn airspeed gleich windspeed ist. ![]()
Schwieriger wird es dann noch, wenn der Wind von der Seite kommt und komplexer wird es, wenn die Strecke viele Abschnitte hat für die es eine gemeinsame Effizienz zu berechnen gilt.
Ziel
Es gilt ein Framework aufzubauen, dass es ermöglicht die Effizienz, und damit auch den Energieverbrauch, für eine gegebene Strecke zu berechnen. Die einzige Eingabe dafür soll die Windrichtung, Windstärke und das Effizienzprofil des verwendeten Flugzeugs in Watt pro km/s sein. Für eine Suchpattern gilt es vorzuschlagen in welche Himmelsrichtung die Flugbahnen ausgerichtet werden, um am effizientesten zu fliegen.
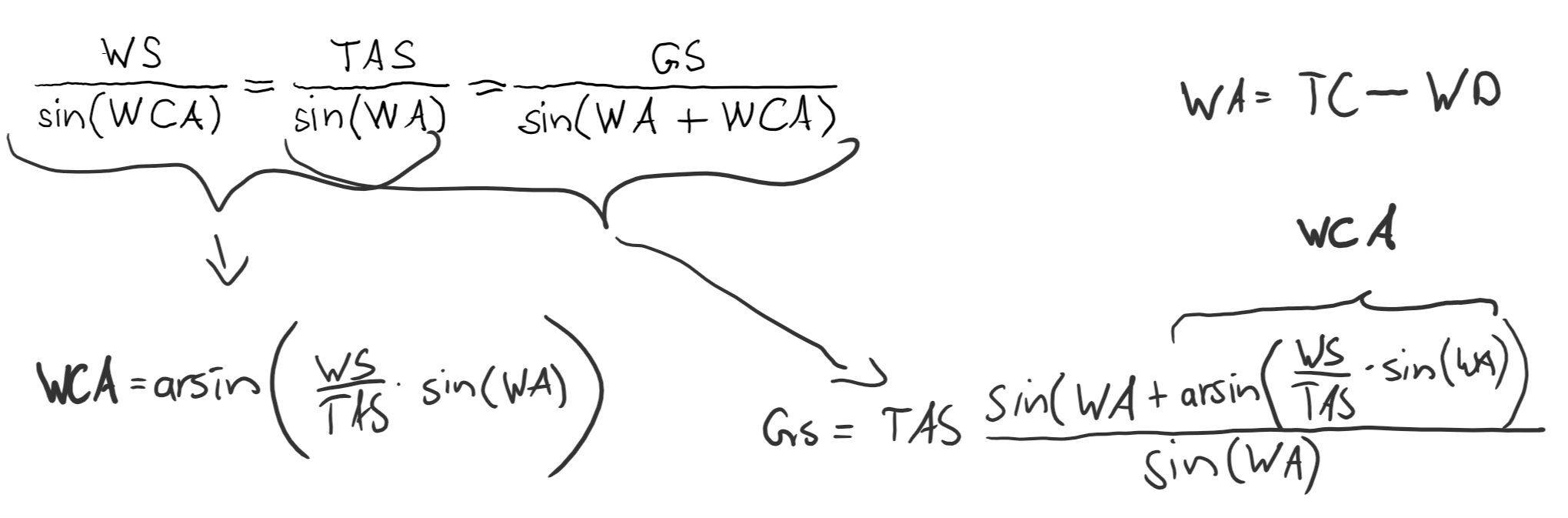
Formeln
Algorithmus
Konzept
- Relativer Windwinkel der Strecken berechnen
Matlab - Skript
Interpolieren der Effizienzwerte
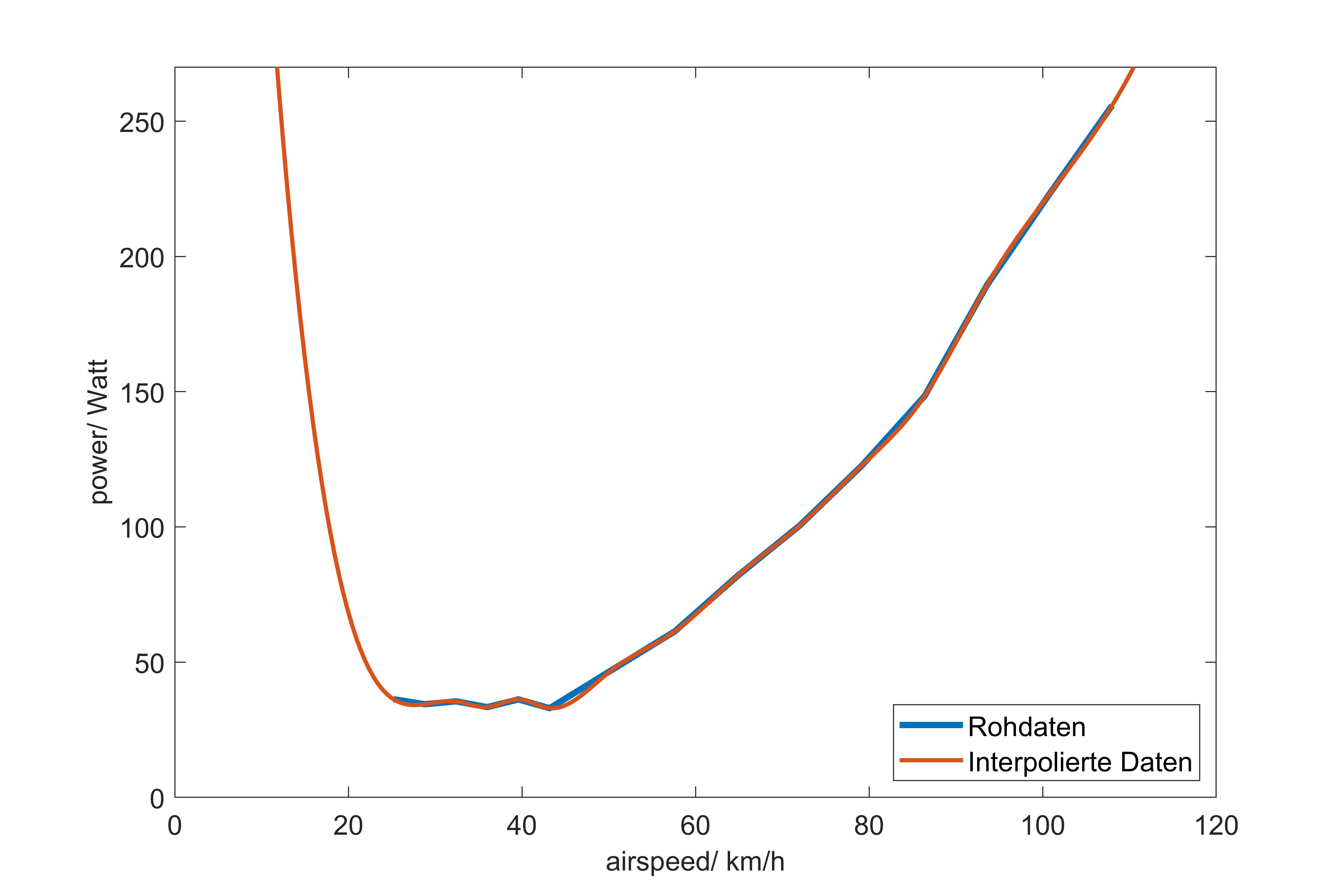
Zum plotten der Kurven und zum genaueren Bestimmen der besten airspeed ist es unerlässlich die durch Messungen erhaltenen Rohdaten zu interpolieren. Zur besseren Darstellung in den plots sind auch Werte für Geschwindigkeiten runter auf 1km/h und etwas höher als die höchste gemessene Geschwindigkeit interessant. Damit diese Extrapolationen die Kurve nicht derart verändern, dass eine fehlerhafte effizienteste Geschwindigkeit ermittelt wird, muss darauf geachtet werdern, dass die extrapolierten Leistungswerte eher ansteigen, als abzufallen. Die interpolationsfunktion interp1 von matlab mit der Methode “spline” ermöglichte dies in diesem Fall. Sollte das mal nicht der Fall sein, können andere Methoden versucht werden.
- Effizienzberechnung_step1_Interpolation.m
clear all, close all measured_airspeed=[7 8 9 10 11 12 14 16 18 20 22 24 26 28 30]*3.6; %in km/h measured_power=[36.28589708 34.42375852 35.50096102 33.3665519 36.21718883 32.94772362 47.17750566 61.33935748 81.75780878 100.4778223 122.7823714 148.3755128 189.4795868 223.162757 255.8001442]; %in Watt N_v=300; %Anzahl der untersuchten Geschwindigkeitspunkte v_a_max=150; %Maximaler airspeed in km/h v_a = linspace(1,v_a_max,N_v); interp_power = interp1(measured_airspeed, measured_power, v_a,'spline'); % %Interpolierte Effizienzkurve plotten plot(measured_airspeed, measured_power, 'linewidth', 3) hold on plot(v_a, interp_power) hold off legend('Rohdaten','Interpolierte Daten' ) xlabel('airspeed/ km/h') ylabel('Power/ Watt') ylim([0 270])
Das Ergebnis der Interpolation ist in diesem Bild zu sehen.
Weitere scripts benutzen den Funktionsaufruf load_aircraft_eff() um die interpolierte Leistungskurve zu laden.
- load_aircraft_eff.m
function [v_a,interp_power] = load_aircraft_eff() %load_aircraft_eff Flugzeugeffizienzkurve laden measured_airspeed=[7 8 9 10 11 12 14 16 18 20 22 24 26 28 30]*3.6; %in km/h measured_power=[36.28589708 34.42375852 35.50096102 33.3665519 36.21718883 32.94772362 47.17750566 61.33935748 81.75780878 100.4778223 122.7823714 148.3755128 189.4795868 223.162757 255.8001442]; %in Watt N_v=300; %Anzahl der untersuchten Geschwindigkeitspunkte v_a_max=150; %Maximaler airspeed in km/h v_a = linspace(1,v_a_max,N_v); %Geschwindigkeitsvektor interp_power = interp1(measured_airspeed, measured_power, v_a,'spline'); end
Berechnung der besten Effizienz
Eine weitere elementare Funktion ist eff_calc. Diese gibt die Geschwindigkeit und die Effizienz zurück, die mit der gegebenen Effizienzkurve möglich sind. Die Effizienz bezieht sich immer auf den windlosen Fall.
- eff_calc.m
function [v_best,res_eff_best] = eff_calc(interp_power,v_a, TC, v_w, WD ) %eff_calc calculates the best speed and best efficiency of the plane for a given %efficiency curve, track, wind speed and wind direction WA = (WD-TC)*pi/180; WA_grad = 180/pi*WA; if WA==0 WA=0.0000001; %durch Null teilen verhindern end if WA==pi || WA==-pi WA=pi*1.00001; %Singularität verhindern end v_a(v_w>v_a) = v_w; %complexe Zahlen verhindern durch |asin_argument| < 1 v_g = v_a.*(sin(WA+asin(v_w./v_a.*sin(WA)))) ./ sin(WA); eff=v_g./v_a; for idx=1:numel(v_a) if eff(idx)<0 || v_w>=v_a(idx) eff(idx) = 0; end end res_eff= v_a./interp_power.*eff.*100./max(v_a./interp_power); %Effizienz des Fliegers (Formel hat ggf. Optimierungspotenzial^^) [~,idx_best] = max(res_eff); v_best = v_a(idx_best); res_eff_best = res_eff(idx_best); %Ergebnis soll Strecke/Energie in % sein (Bezug auf Windstille) figure(1) plot(v_a, res_eff); hold on plot(v_a(idx_best), res_eff_best, 'marker','x'); xlabel('airspeed/ km/h') ylabel('efficiency / %') end
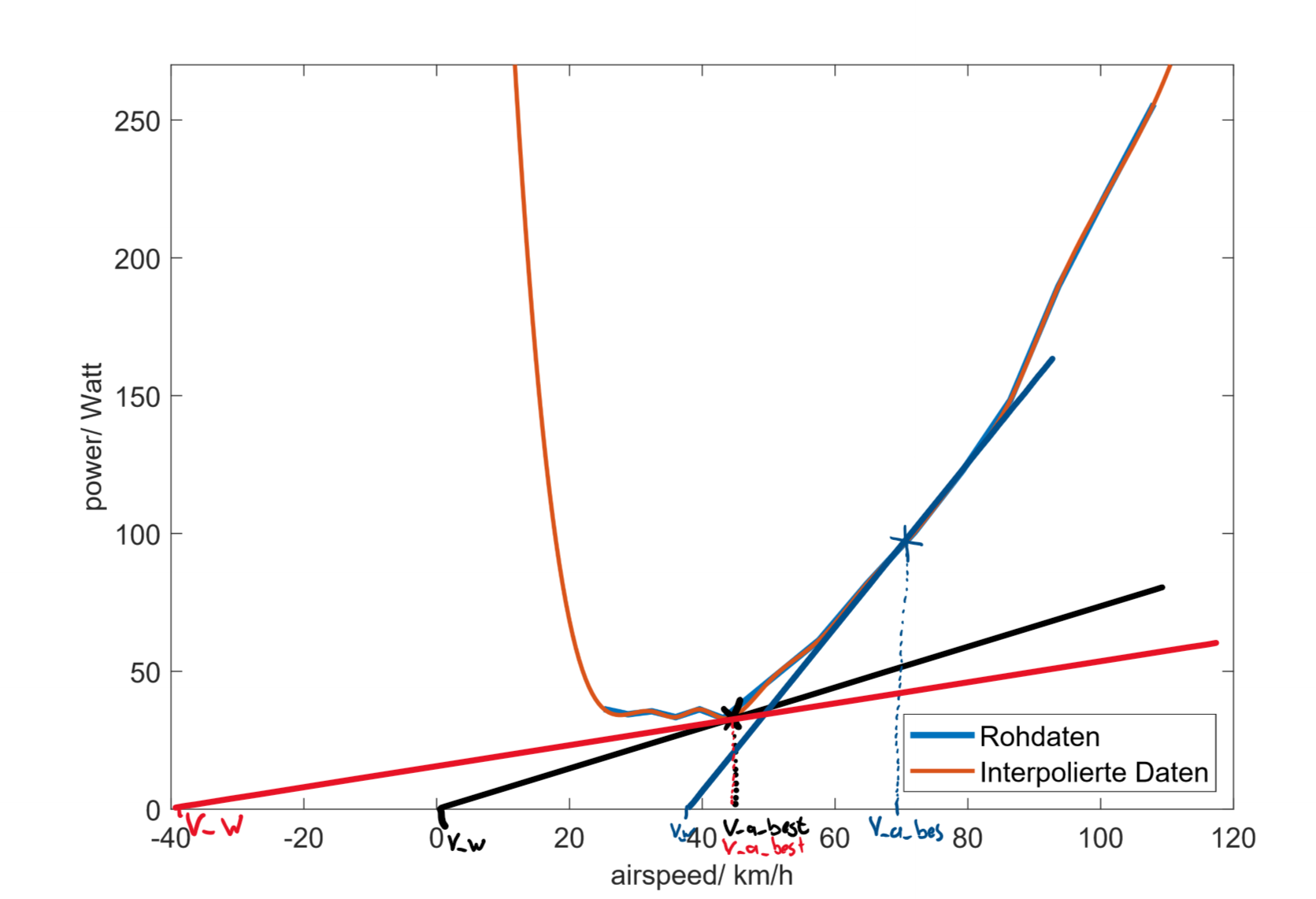
Für den vereinfachten Fall “Flug gegen den Wind” kann man die beste airspeed sogar recht anschaulich ermitteln. Im folgenden Bild wird gezeigt, wie man durch Geraden, die ihre Ursprünge in der jeweiligen windspeed haben, die Geschwindigeit der besten Effizienz ermitteln kann. Dabei fällt auf, dass negative Winde gegen die Flugrichtung die Geschwindigkeit der besten Effizienz nicht beeinflussen. Erst ab einer Geschwindigkeit von ca. 35km/h wandert die Geschwindigkeit der besten Effizienz nach oben.
Effizienz bei Variation der Windgeschwindigkeit
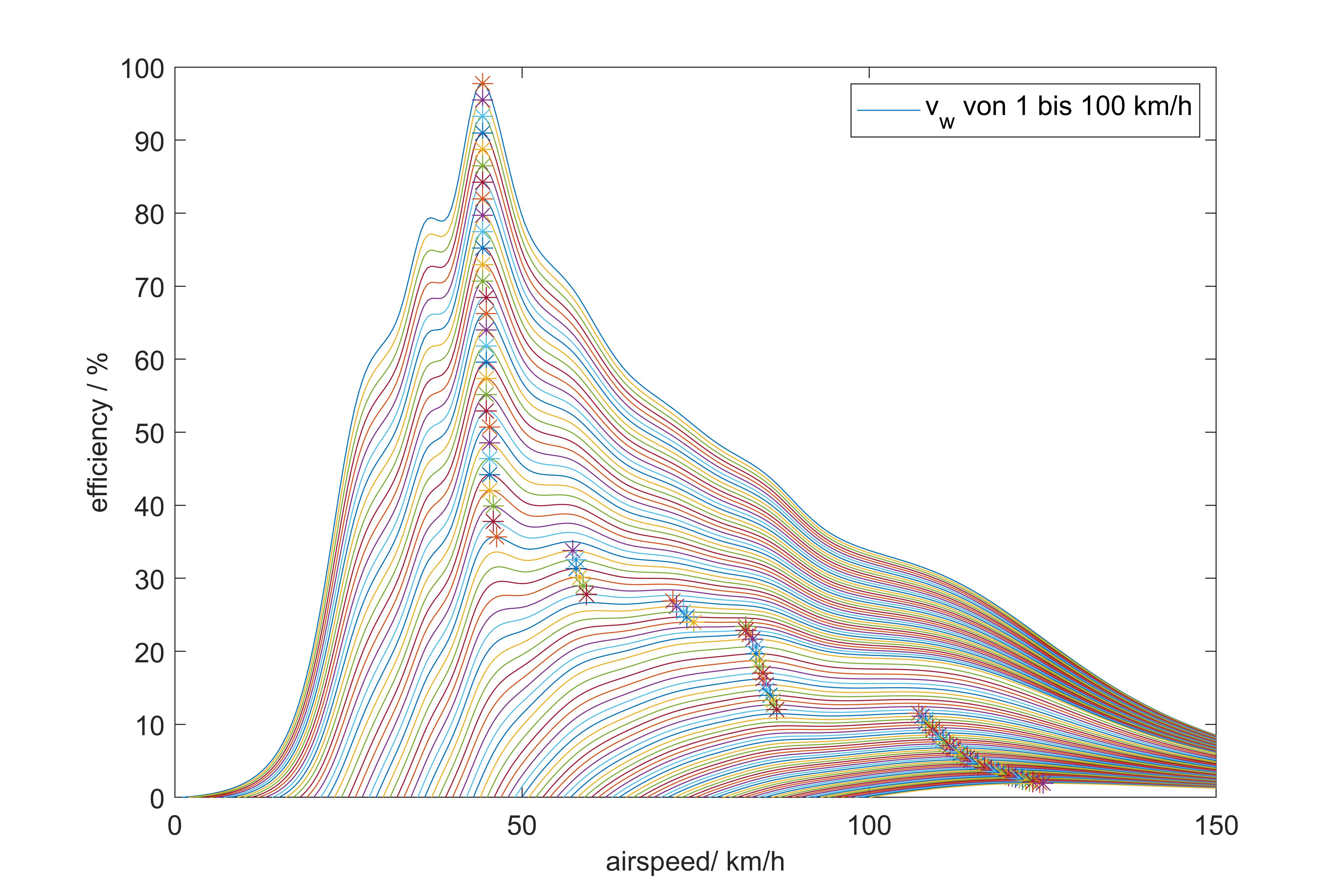
Mit dem script Effizienzberechnung_Windspeedvariation.m ist es möglich die efficiency für eine Schaar aus Windgeschwindigkeiten zu ermitteln. In diesem Fall wurde eine winddirection von 180° bei einem true course von 0° gewählt (also Gegenwind). Die windspeed wurde von 1 bis 100km/h in 1km/h-Schritten variiert.
- Effizienzberechnung_Windspeedvariation.m
clear all, close all [v_a,interp_power] = load_aircraft_eff(); v_w=40; %windspeed in km/h WD=-180; %winddirection in ° TC=0; %true course in ° for v_w=1:100 [v_best,res_eff_best(v_w)] = eff_calc(interp_power,v_a, TC, v_w, WD ); end legend('v_w von 1 bis 100 km/h' ) figure(2) plot(1:100,res_eff_best, 'linewidth', 3); xlabel('windspeed/ km/h') ylabel('efficiency / %')
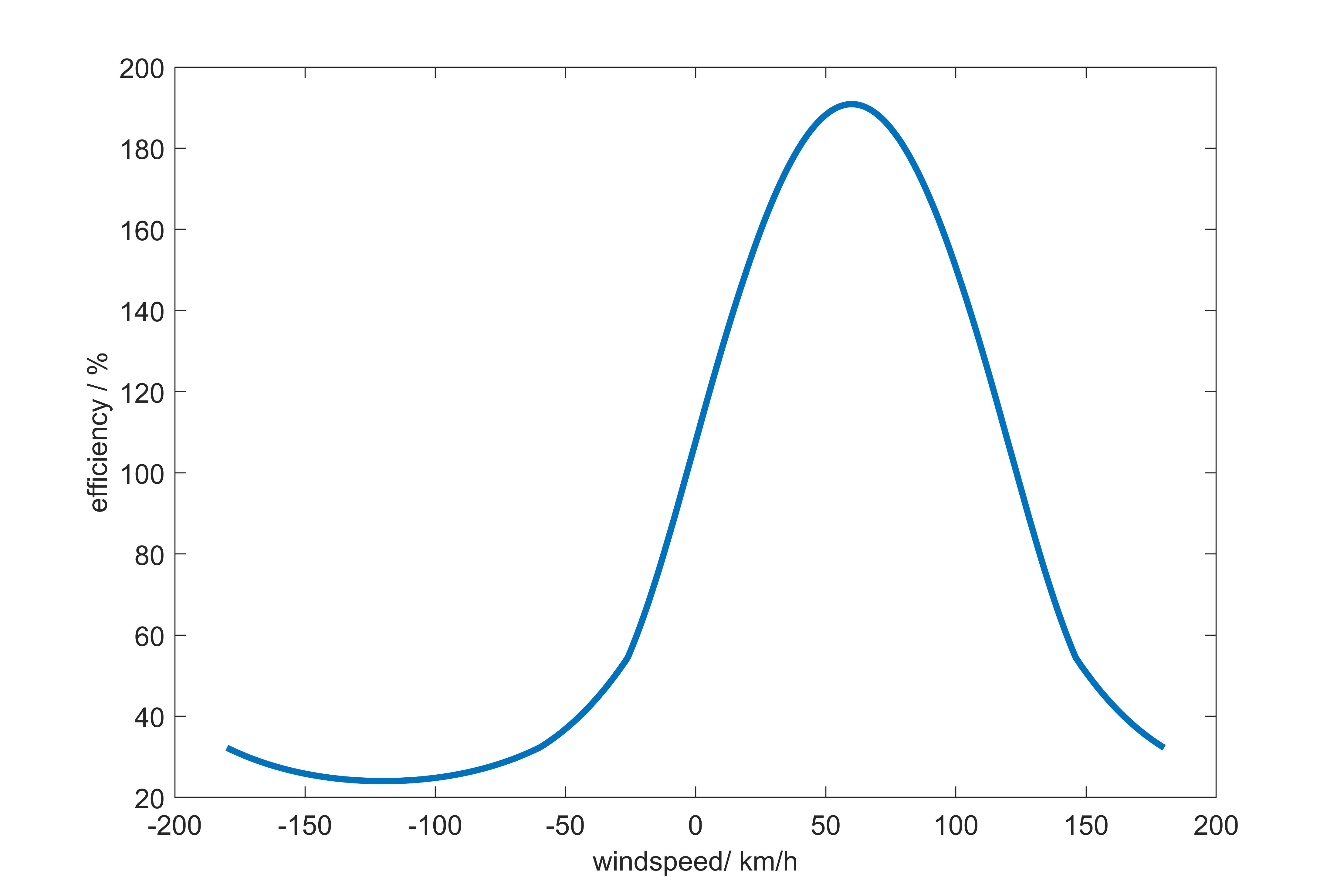
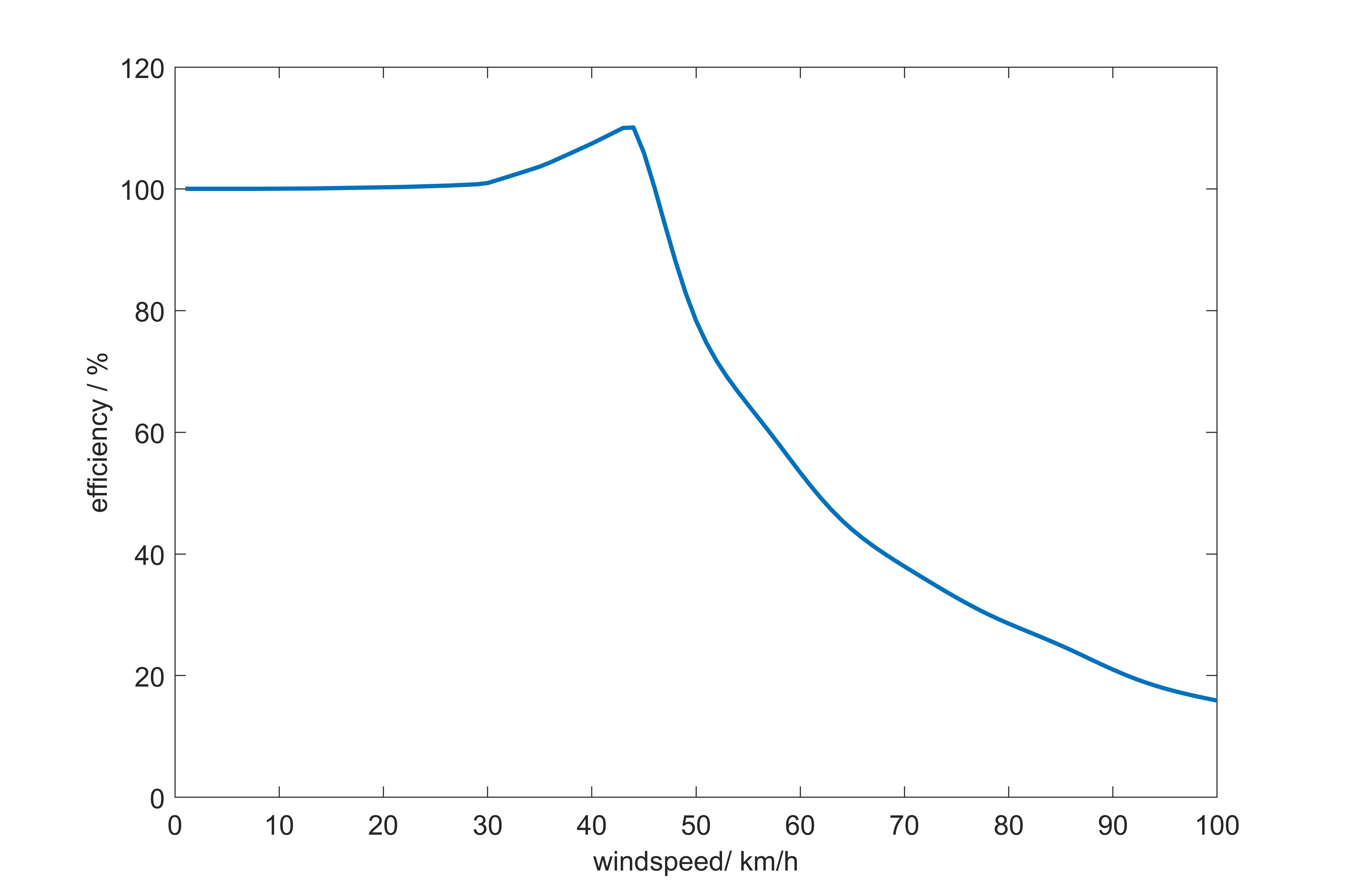
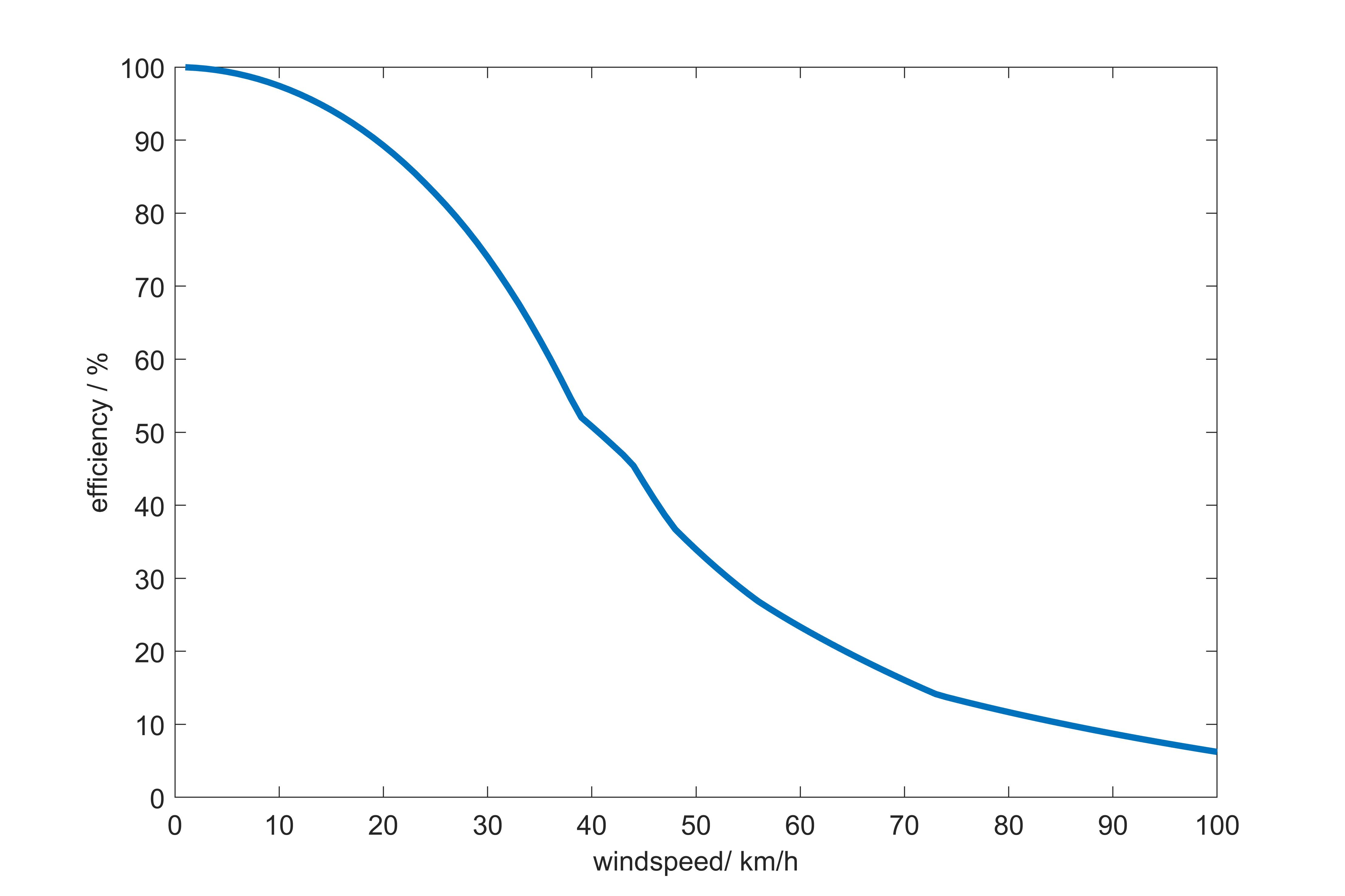
Schön zu sehen sind die Sprünge der besten Geschwindigkeit, die der Welligkeit der interpolierten Effizienzkurve geschuldet sind. Folgender Verlauf der Effizienz in Abhängigkeit der Windgeschwindigkeit ergeben sich dabei. Bei dem Wind handelt es sich um Gegenwind, also Wind direkt auf die Nase des Flugzeugs.
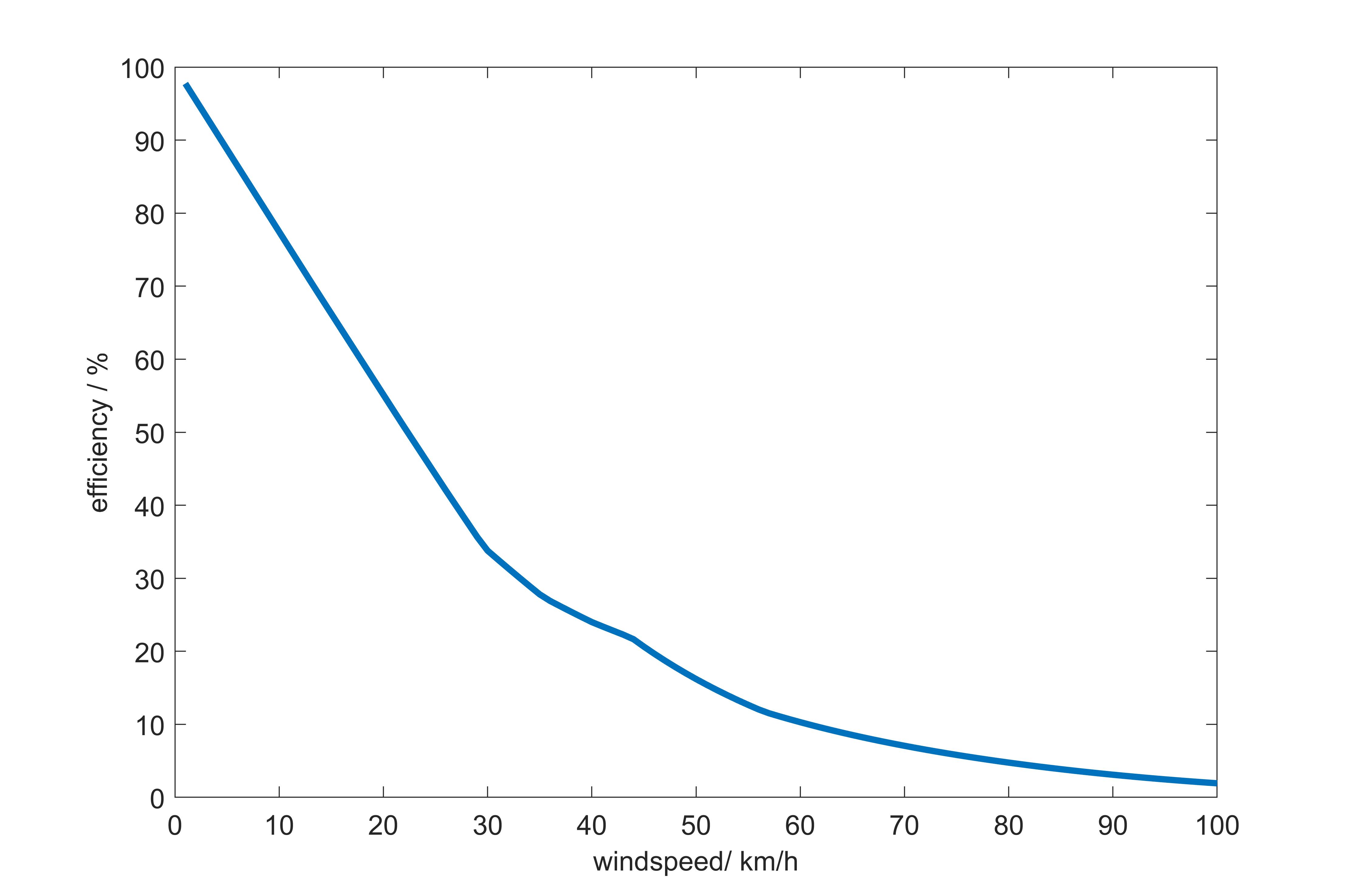
Bei einem Wind von 90 von der Seite ergibt sich eine andere Kurve für die Effizienz in Abhängigkeit der Windgeschwindigkeit. Wie man im folgenden Bild sieht, dropped die Effizienz erst bei höheren Windgeschwindigkeiten steil ab und hat einen eher schwachen Einfluss bei geringen Windgeschwindigkeiten.
Effizienz bei Variation der Windrichtung
Der Einfluss der wind direction bei konstantem windspeed lässt sich mit folgendem script darstellen.
- Effizienzberechnung_Windspeedvariation.m
clear all, close all [v_a,interp_power] = load_aircraft_eff() v_w=40 ; %windspeed in km/h WD=60 ; %winddrection in ° for TC=-180:180 [v_best,res_eff_best(TC+181)] = eff_calc(interp_power,v_a, TC, v_w, WD ); end legend('TC von -180° bis 180°' ) figure(2) plot(-180:180,res_eff_best, 'linewidth', 3); xlabel('windspeed/ km/h') ylabel('efficiency / %')
Die Plots ähneln dem Verlauf bei der Windgeschwindigkeitsvariation. Der windspeed ist hierfür auf 40 km/h eingestellt und die wind direction liegt bei 60°.
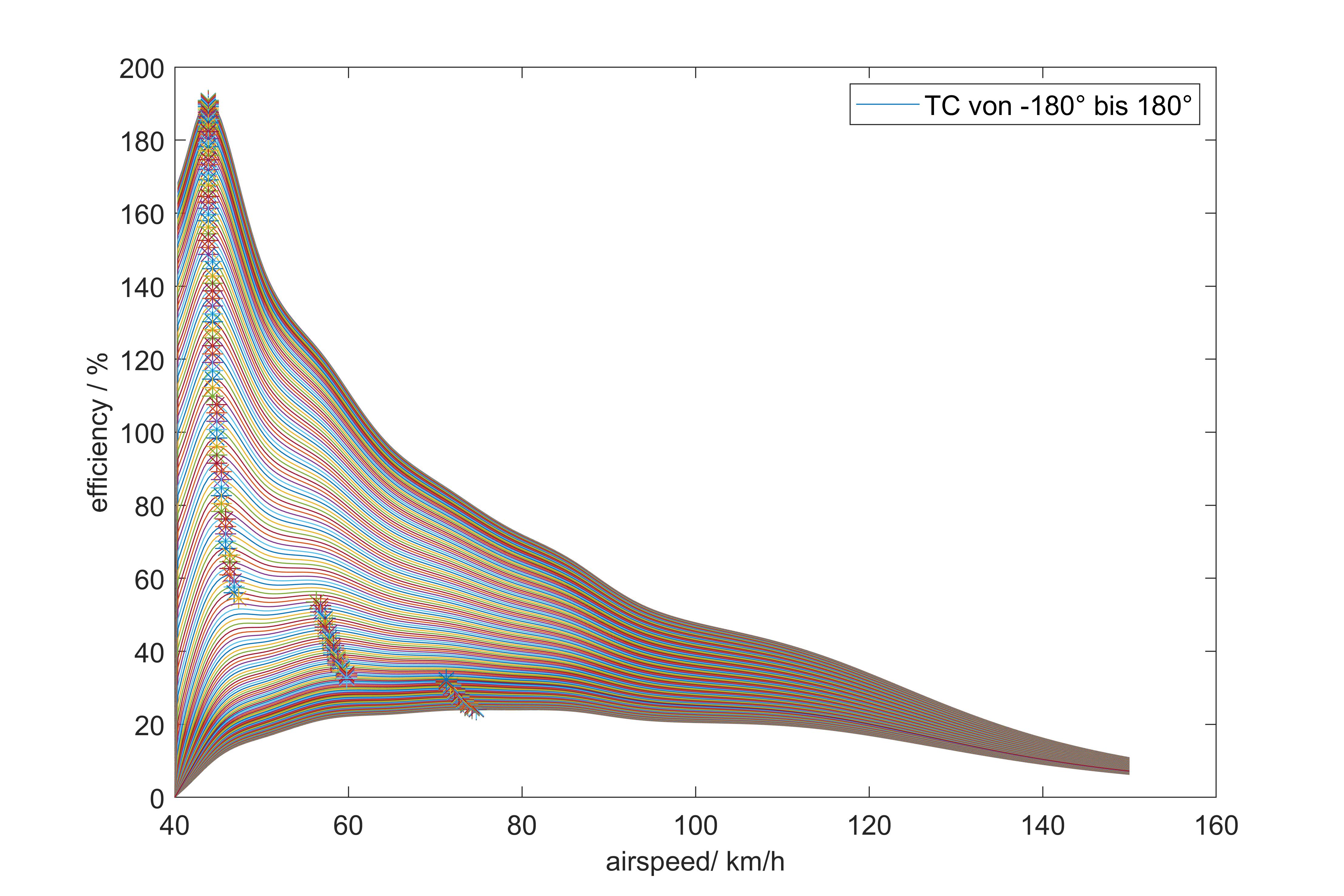
Beste Effizienz bei Rückenwind…keine Überraschung, aber schön zu sehen, dass das Model stimmt.
- Effizienzberechnung_Flugplan.m
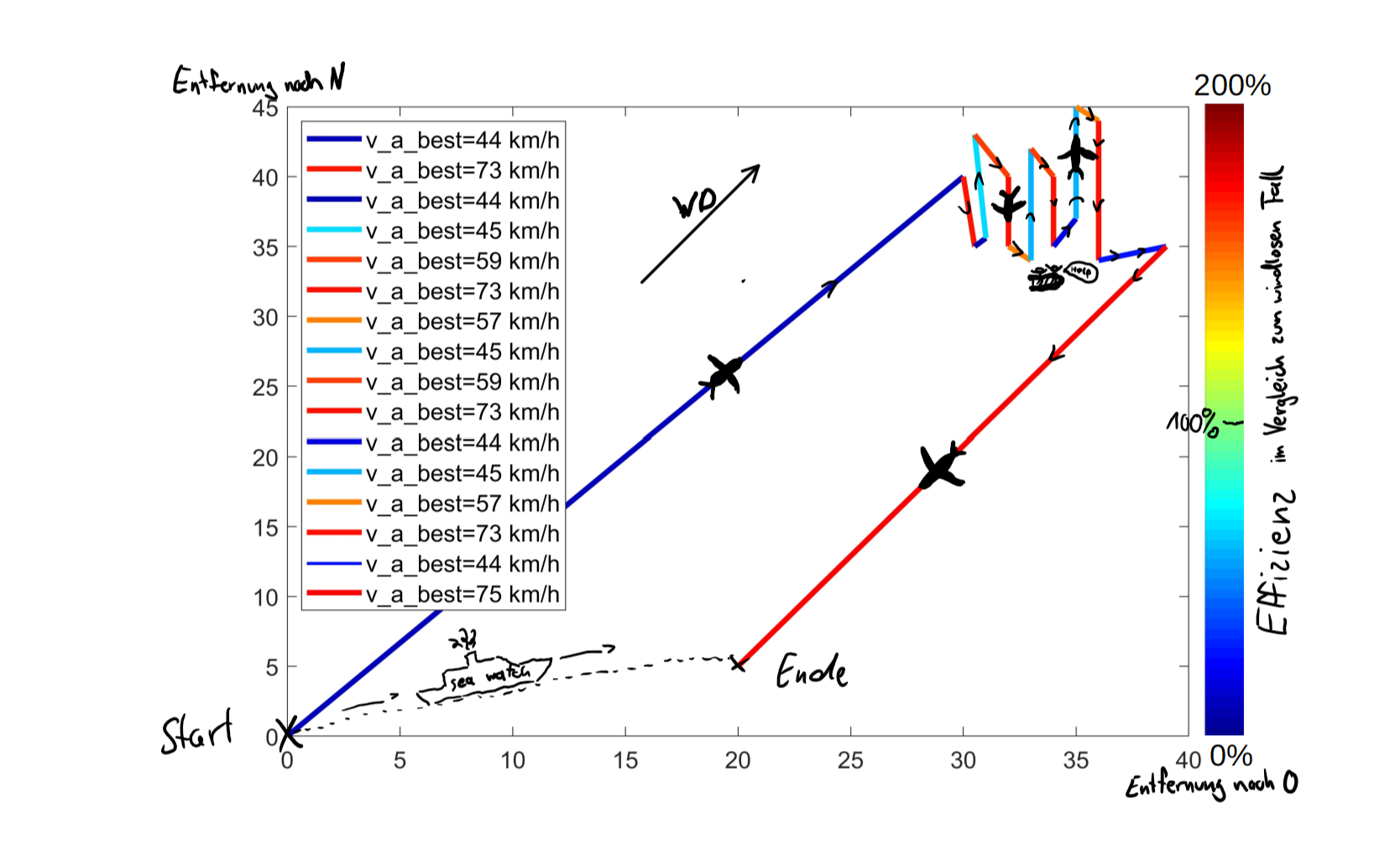
clear all, close all [v_a,interp_power] = load_aircraft_eff() % % %Interpolierte Effizienzkurve plotten % plot(measured_airspeed, measured_power, 'linewidth', 3) % hold on % plot(v_a, interp_power, 'linewidth', 2) % hold off % legend('Rohdaten','Interpolierte Daten','location','southeast' ) % xlabel('airspeed/ km/h') % ylabel('power/ Watt') % ylim([0 270]) % xlim([-40 120]) v_w=40; %windspeed in km/h WD=45; %windangle in ° %Track points typischer Flug P_x = [0 30 30.5 31 30.5 32 32 33 33 34 34 35 35 36 36 39 20]; P_y = [0 40 35 35.6 43 40 35 34 42 40 35 37 45 44 34 35 5]; % %Track points im Kreis % P_x = [0 1 2 2 1 0 -1 0]; % P_y = [0 1 1 0 -1 -1 0 0]; %Track points einmal hin und her P_x = [0 1 0 ]; P_y = [0 0 0 ]; trip_length=0; for track=1:(numel(P_x)-1) %optional zum debuggen % figure(4) % h = plot([P_x(track) P_x(track+1)] , [P_y(track) P_y(track+1)], 'linewidth', 3); % hold on TC=(atan2d((P_x(track+1)-P_x(track)),(P_y(track+1)-P_y(track)))); track_length(track)= sqrt((P_y(track+1)-P_y(track))^2+(P_x(track+1)-P_x(track))^2); [v_best(track),res_eff_best(track)] = eff_calc(interp_power,v_a, TC, v_w, WD ); trip_length=trip_length+track_length(track); end figure(2) colorbar_eff=jet(200); trip_eff=0; for track=1:(numel(P_x)-1) trip_eff = trip_eff + track_length(track)/trip_length*res_eff_best(track); h = plot([P_x(track) P_x(track+1)] , [P_y(track) P_y(track+1)], 'linewidth', 3); hold on set(h, 'color', squeeze((colorbar_eff(ceil(200-res_eff_best(track)),:)))); end trip_eff legendCell = cellstr(num2str(ceil(v_best)', 'v\\_a\\_best=%-d km/h')); legend([legendCell],'location', 'northwest');
trip_eff = 105.8751 ….wie kann das sein? Liegt es am Pfad? Wie kann man besser sein, als ohne Wind?
Neuer Flugplan: 1 nach Ost und dann wieder 1 nach West bei Westwind
Ergebnis: trip_eff = 107.4352
Gleicher Flugplan bei v_w=44;
Ergebnis: trip_eff = 110.0722
v_w=50; Ergebnis: trip_eff = 78.3424
Das schreit doch nach einer weiteren Variation. Also bei Seitenwind kommt das gleiche raus wie oben bei der Windvariation bei TC=90°. Aber was kommt raus, wenn der Wind bei Hin- und Rückflug mal von vorne und mal von hinten kommt, wenn man die Geschwindigkeit auf die beste Effizienz anpasst?
Kaum zu glauben, es gibt wohl echt ein Fenster, in dem man effizienter fliegt, wenn es Wind gibt.
Implementierungsmöglichkeit für QGroundControl
- Feld ergänzen
- Ausgabe erweitern
Abschätzung des Effizienzvorteils durch die Implementierung
Am naheliegensten ist die Betrachtung eines typischen Suchflugs bei typischen Windbedingungen. Dafür wird zunächst der vereinfachte Flugplan von oben verwendet mit einem etwas über dem Durschnitt liegenden Meerwind von 6bft (also ~44km/h). Das framework gibt die Effizienz im Bezug zu Windlosigkeit an. Wir würden gerne die Effizienz im Bezug zu Effizienz ohne optimierter Fluggeschwindigkeit ermitteln.
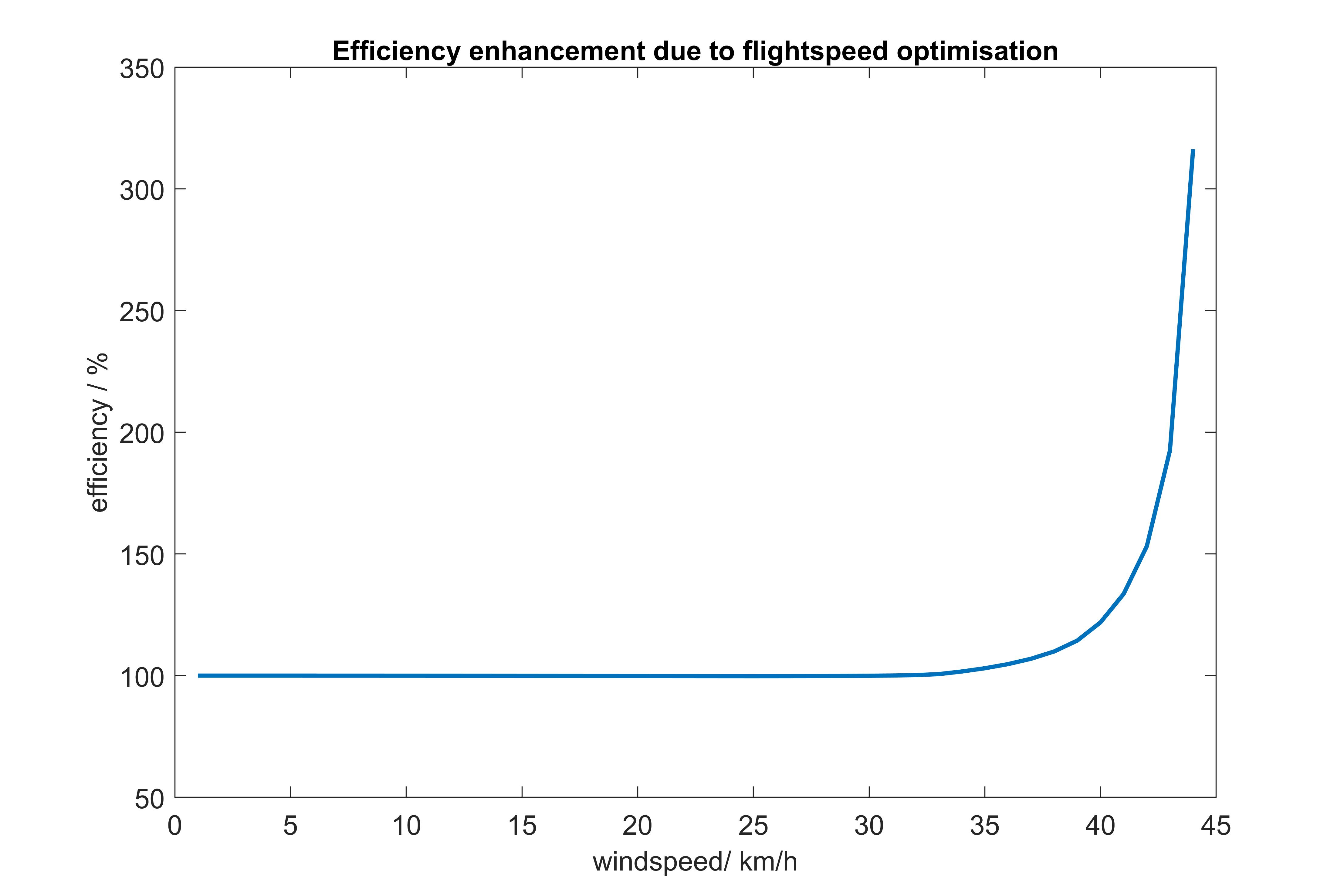
Zu beachten: Durch Variation der Groundspeed, verändert sich auch das Zeitinterval für den Fotoauslöser! (alternativ kann er auch auf den maximalen Groundspeed eingestellt werden.)
== Noch Fragen? == — Christian Panhans 2018/11/19 21:39